ここでは、「どのパラメータが打率等にどれくらい関係するのか」を理解することで強いチームを作る指針を記載しておきます。
[Meisyo]ビッグデータから学ぶ試合の基礎設計4の詳細版です。
今回は、右打と左打はパラメータの相関関係に違いがあるのか？という問いに答えたいと思います。
まずは「右打、左打で平均打率に違いがあるのか？」という問いですが、
R(73867打席):0.2428
L(39563打席):0.2468
左打席に+1.6%補正があるようです。
（とはいえ前回の論文（1割近く）と比べそんなに変わらない結果でした）
コードでは、左打席が右打席に比べ一塁ベースに1m近いです。
正しい結果ですね。
では、どのパラメータが打率に本当に相関しているのか？を単回帰分析で求め、
相関しているパラメータ群を重回帰分析して、各パラメータの相関度合いを確認します。
あとはOPS、HR率なども調査しておきました。改良した分析用コードも載せておきますね！
打率の各パラメータの相関関係
図の見方
タイトル：「Result(***) vs Param(xxx) from pa >= 20」
結果（***）へのパラメータ（xxx）の相関図（20打席（pa）以上）
Right-Hand：右打、Left-Hand：左打
R^2＝決定係数。0～1を取る。1に近いほど相関していると言える。
（>=0.010が2つで相関あり○、1つで相関あり△、なしで相関なし×）
一覧表：
| パラメータ | 相関± | 右打R^2 | 左打R^2 | 相関 |
|---|---|---|---|---|
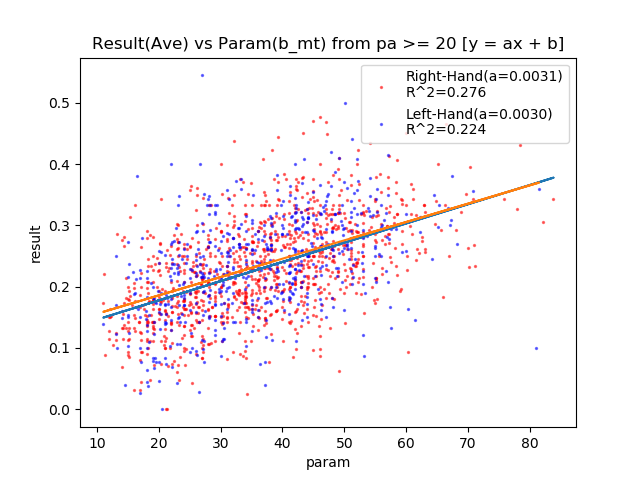
| b_mt | + | 0.276 | 0.224 | ○ |
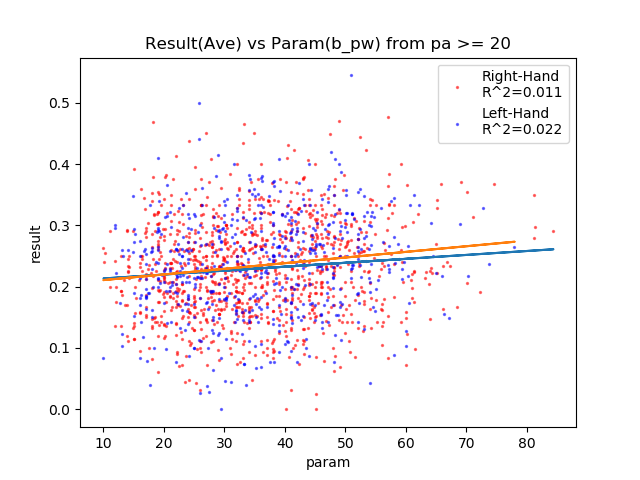
| b_pw | + | 0.011 | 0.022 | ○ |
| b_sp | ? | 0.001 | 0.002 | × |
| b_sf | – | 0.008 | 0.009 | × |
| b_df | – | 0.018 | 0.009 | △ |
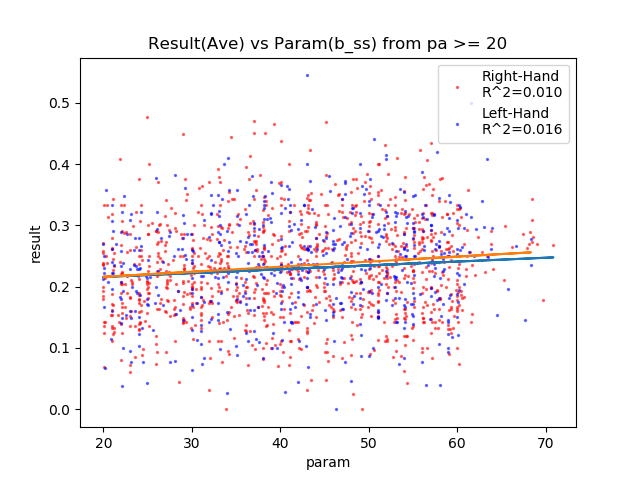
| b_ss | + | 0.010 | 0.016 | ○ |
| b_er | – | 0.002 | 0.000 | × |
| lv | + | 0.021 | 0.014 | ○ |
| cond | + | 0.014 | 0.008 | △ |
| type_b | ? | 0.003 | 0.000 | × |
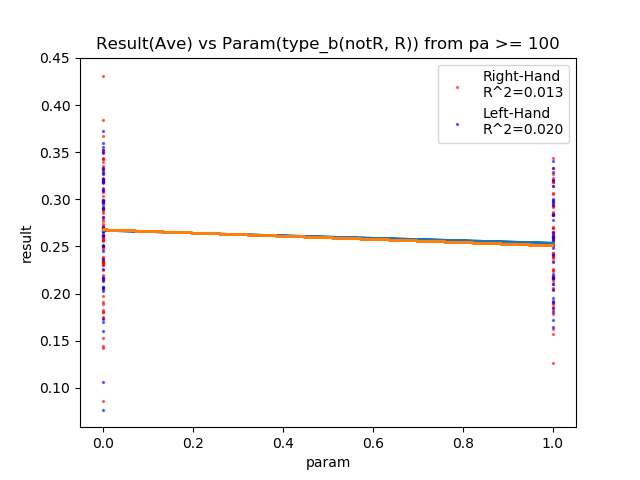
| type_b(R) | – | 0.013 | 0.020 | ○ |
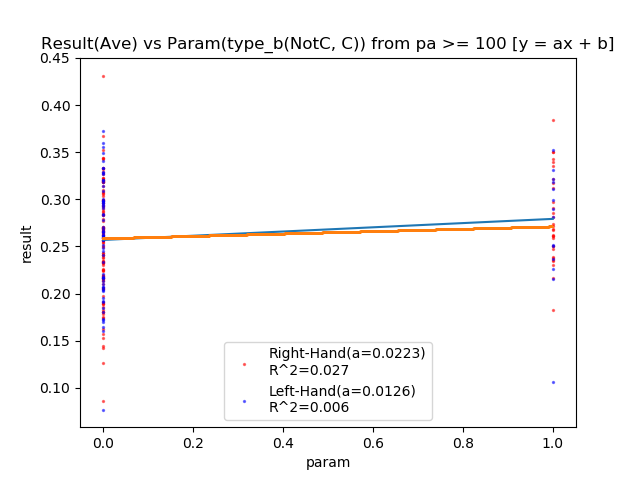
| type_b(C) | + | 0.027 | 0.006 | △ |
| type_b(F) | ? | 0.000 | 0.007 | × |
b_mt、b_pw、b_ssが相関している。
lv（レベル）とcond（調子）は上がれば上がるほど、上記3つのパラメータが上がるので相関するはずという見込みで計算しました。
その通りでした。
type_b（打席位置：隠しパラメータ）は、R（後ろ）がマイナスに相関、C（中央）がプラスに相関△、F（前）が相関なし。
Rは剛速球対応用で、Fが超変化球対応用として設計しました。Rは変化球に弱く、Fは速球に弱いという裏設計ですね。
現在はC=F>Rです。速球投手が増えればRが台頭してくるはず！
重回帰分析：
Ave(R)
Name Coefficients
2 b_ss 0.000343
1 b_pw 0.000550
0 b_mt 0.003096
切片：0.08263525884539452
Ave(L)
Name Coefficients
2 b_ss 0.000450
1 b_pw 0.000852
0 b_mt 0.002925
切片：0.07878629626174283
各相関図：
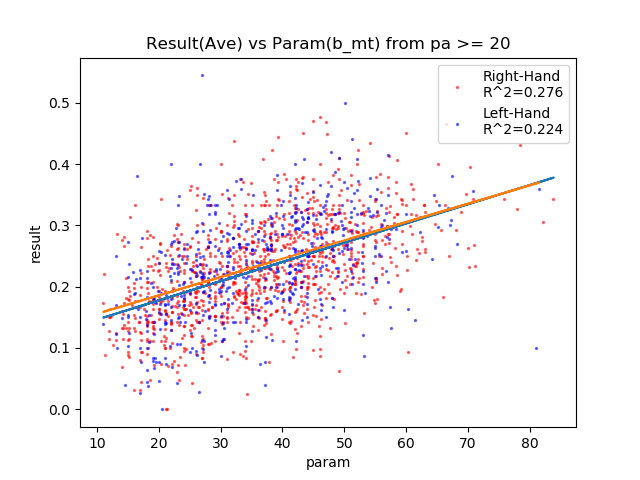
ミートはとてもキレイな相関図になってます。
左右どちらも変わらないんですね！
パワーは相関してる・・・？相関してるか。みたいな図ですね。
走力は相関なし。
不思議です。要調査ですね。
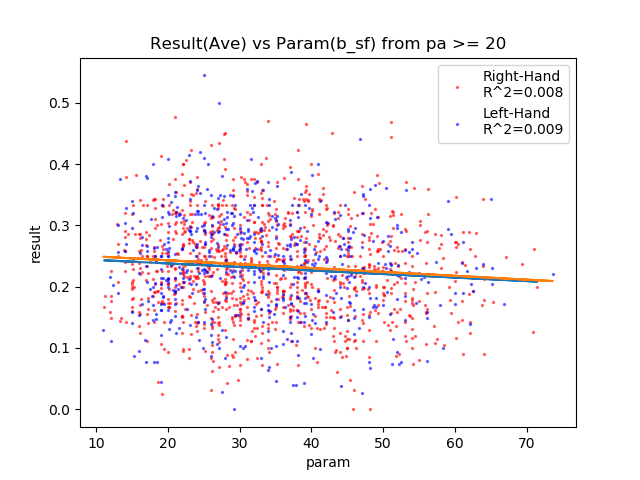
肩力は相関なし。
マイナス相関してそうに見えます。肩が上がればその分ミートとパワーが下がるしね。
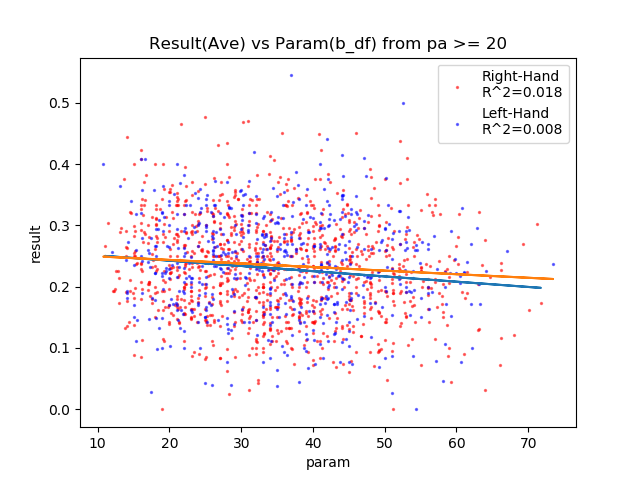
守備力は相関あり△。
マイナス相関してそうに見えます。守備が上がればその分ミートとパワーが下がるしね。
反応は相関あり。
あまり偏回帰係数は大きくなさそう。
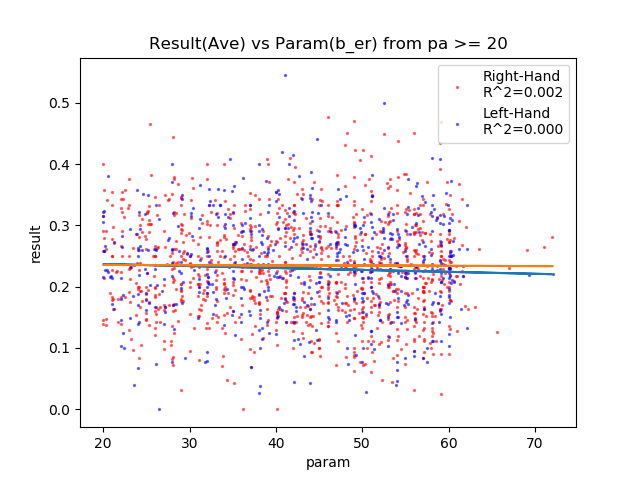
エラー回避は相関なし。
反応とエラー回避はランダムで決定される（＝その他のパラメータから独立している）ので、そんなものですね。
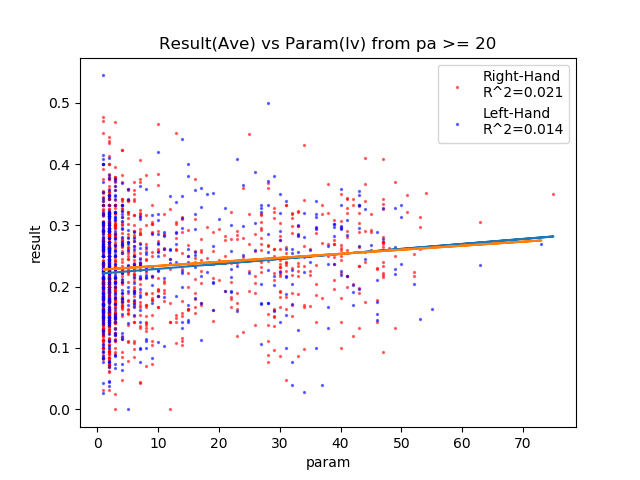
選手Lvが上がれば打率が上がる！
育成での能力アップと、打てない人はそれまでに淘汰されてるしわかるかな。
・・・Lv70とか誰だ？
調子は相関あり△。
調子は経時変動あるから実際わからない。
R（-1）、C（0）、F（+1）として設定。
相関なし。
Rはマイナスに相関。（NotR＝C,F）
Cはプラスに相関。（NotC＝R,F）
Fは相関なし。（NotF＝R,C）
これは不思議ですね。
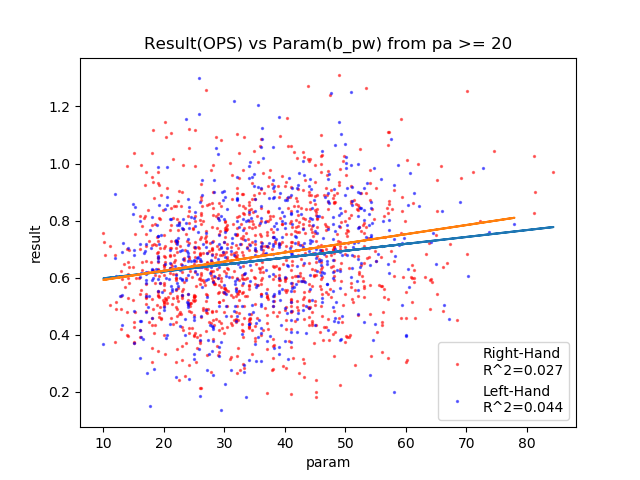
OPSの各パラメータの相関関係
一覧表：
| パラメータ | 相関± | 右打R^2 | 左打R^2 | 相関 |
|---|---|---|---|---|
| b_mt | + | 0.218 | 0.183 | ○ |
| b_pw | + | 0.027 | 0.044 | ○ |
| b_sp | ? | 0.001 | 0.001 | × |
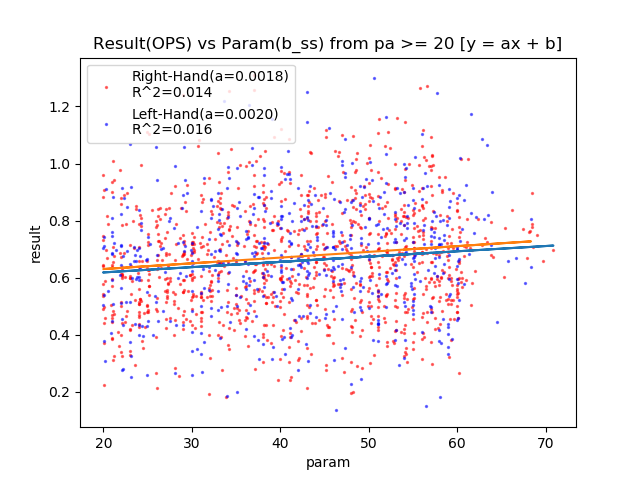
| b_ss | + | 0.014 | 0.016 | ○ |
これもミートが圧倒してますね・・・。
重回帰分析：
OPS(R)
Name Coefficients
2 b_ss 0.001203
1 b_pw 0.002206
0 b_mt 0.006626
切片：0.28842150643875264
OPS(L)
Name Coefficients
2 b_ss 0.001145
1 b_pw 0.003046
0 b_mt 0.006414
切片：0.28466512542137623
左右の違いがわからない。
各相関図：
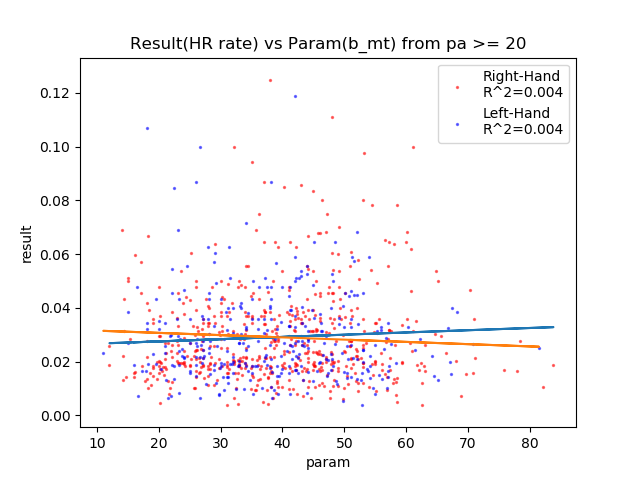
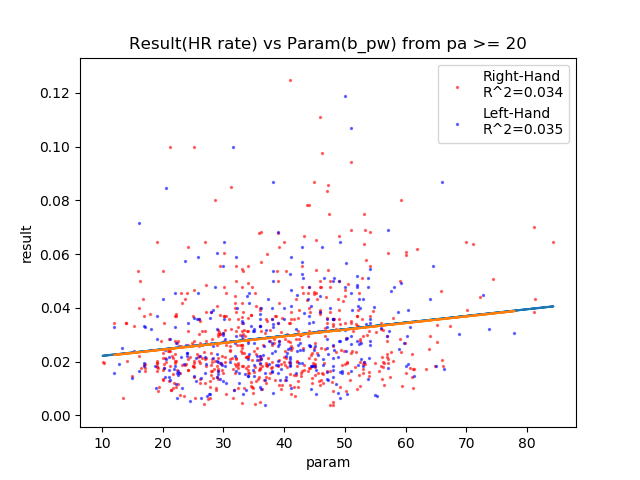
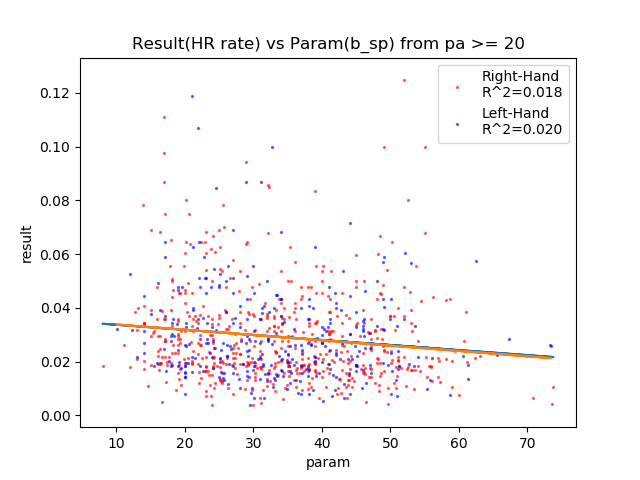
HR率の各パラメータの相関関係
結果：
やっぱりパワーだけしか相関しなかった。
ただしパワー100でもそんなにHR率は上がらない。悲しい。
各相関図：
コード
# -*- coding: utf-8 -*-
import os, sys, csv
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
# 基礎設定
file_name = 'meisyo_b 20181217.csv'
# CSV読み込み
df = pd.read_csv(file_name, encoding='utf-8')
# 投手能力結合・削除
for i in ['sp', 'co', 'st', 'bb1n', 'bb2n', 'bb3n']:
df['p_'+i] = df['p_'+i] + df['pt_p_'+i] + df['pw_p_'+i]
df = df.drop(['pt_p_'+i, 'pw_p_'+i], axis=1)
# 野手能力結合・削除
for i in ['mt', 'pw', 'sp', 'sf', 'df', 'er', 'ss']:
df['b_'+i] = df['b_'+i] + df['pt_b_'+i] + df['pw_b_'+i]
df = df.drop(['pt_b_'+i, 'pw_b_'+i], axis=1)
# 欠損値のある行を把握
# print(df.isnull().sum())
# 全体で欠損値のある行を削除
df = df.drop(['skill', 'g_pos', 'grow_type'], axis=1)
# 打席数*未満を削除
df = df.where(df['ab'] >= 20).dropna()
#df['type_b'] = df['type_b'].replace({'F': 1, 'C': 0, 'R': 0})
# R/L
R = df.where(df['side_b'] == 'R').dropna()
L = df.where(df['side_b'] == 'L').dropna()
# データ把握
# print(df.columns)
# print(df.head())
# print(R.head())
# print(L.head())
# print("R(" + str(sum(R['ab'])) + "):"+ str(sum(R['h']) / sum(R['ab'])))
# print("L(" + str(sum(L['ab'])) + "):"+ str(sum(L['h']) / sum(L['ab'])))
# 結果出力
dR = pd.DataFrame(index=[], columns=[])
dL = pd.DataFrame(index=[], columns=[])
dR['ave'] = R['h'] / R['ab']
dR['obp'] = (R['h'] + R['bb'] + R['hbp']) / (R['ab'] + R['bb'] + R['hbp'] + R['sf'])
dR['slg'] = R['tb'] / R['ab']
dR['ops'] = dR['obp'] + dR['slg']
dL['ave'] = L['h'] / L['ab']
dL['obp'] = (L['h'] + L['bb'] + L['hbp']) / (L['ab'] + L['bb'] + L['hbp'] + L['sf'])
dL['slg'] = L['tb'] / L['ab']
dL['ops'] = dL['obp'] + dL['slg']
yR = dR.values[:, 0]
yL = dL.values[:, 0]
# 相関係数
list = ['b_mt']
xR = R.loc[:, list].values
xL = L.loc[:, list].values
# title
plt.title("Result(Ave) vs Param(b_mt) from pa >= 20 [y = ax + b]")
plt.xlabel("param")
plt.ylabel("result")
# plt 回帰係数
model_R = linear_model.LinearRegression()
model_L = linear_model.LinearRegression()
model_R.fit(xR, yR)
model_L.fit(xL, yL)
# plt 散布図
plt.scatter(xR, yR, s=2, c="red", alpha=0.5, label="Right-Hand(a="+str("{0:.4f}".format(model_R.coef_[0]))+")\nR^2="+str("{0:.3f}".format(model_R.score(xR, yR))))
plt.scatter(xL, yL, s=2, c="blue", alpha=0.5, label="Left-Hand(a="+str("{0:.4f}".format(model_L.coef_[0]))+")\nR^2="+str("{0:.3f}".format(model_L.score(xL, yL))))
# plt 回帰
plt.plot(xR, model_R.predict(xR))
plt.plot(xL, model_L.predict(xL))
print("Ave(R)")
print(pd.DataFrame({"Name":list, "Coefficients":model_R.coef_}).sort_values(by='Coefficients') )
print(model_R.intercept_)
print("Ave(L)")
print(pd.DataFrame({"Name":list, "Coefficients":model_L.coef_}).sort_values(by='Coefficients') )
print(model_L.intercept_)
# show
plt.legend()
plt.show()
sys.exit()
ひとこと
図示することは大事ダナーと思いました。
だって数値だけでは全然わかりませんから！
出た数値を使って歴代優勝校の選手を生成します。(^q^)
