統計的因果推論の一分野である統計的因果探索。
その研究の中で生み出された画期的なモデルLiNGAMの解説を行います。PythonによるLiNGAMの実装については、cdt15/lingamと、応用モデルおよびPythonモジュールの解説をご覧ください。
背景
これまでの統計学や機械学習の多くが、相関を元に関係性を把握してきました。
ただし、その変動は何が原因なのかという本当に知りたいことは不明でした。
因果探索とは、データから因果構造を推定する方法を指します。
それは、因果の方向性や大きさを含み、これまでの統計学や機械学習とは違った原因とは何かを探していく方法です。
ここでは、統計的因果探索の代表的なアプローチであるLiNGAM(Linear Non-Gaussian Acyclic Model)を紹介します。
数理的なアプローチは他の資料に譲るとして、実用にはどういった点を注意すべきか、どのような応用モデルがあるかについて中心に説明します。
LiNGAM適用の前提条件
LiNGAMを適用する前に、適用するデータの前提条件が4つあります。
(1)Linear
線形な(足し合わせで表現できる)構造方程式で示すことができるとする。
構造方程式とは、下記のような式です。

簡略化するとxは何で、yは何で表されるかを示すことができる式です。
(2)Non-Gaussian
構造方程式の誤差項は非正規(ガウス)分布である。
(3)Acyclic
非循環な因果グラフ(Directed Acyclic Graph)で表すことができるとする。
(4)構造方程式
未観測の要因が存在しない。つまり、構造方程式で因果構造全てを表すことが可能であるとする。
各誤差項は互いに独立であり、各変数は連続値であるとする。
*各誤差項はxやyなどで表せていない値の動きを全て表現できるとする。
調べていて、かなり強い前提を置いているのでは?というところが分かりました。
前提条件の理由
前提は4つありますが、一番気になるのはなぜ「構造方程式の誤差項は非正規(ガウス)分布である。」のかでしょう。
*変数の独立性や分布のガウス性の成否は、一般的な方法で求めることができるので割愛します。
少し調べてみるとLiNGAMはセミパラメトリックアプローチとされています。セミパラメトリックアプローチの定義は、関数型には仮定を置くものの、構造方程式の誤差項(外生変数ともいう)の分布には仮定を置きませんとされています。
LiNGAMは誤差項を「正規分布以外」という仮定であるので、それ以外の分布はすべて取りうる(=仮定を置いていないのと同じ)というスタンスを取っているため、セミパラメトリックアプローチに分類されています。
そうすると、何が嬉しいのでしょうか?
そうしなければ、何に困るのでしょうか?
答えは、誤差項が正規分布であると因果の方向が推定できないのです。
下記の図をご覧ください。
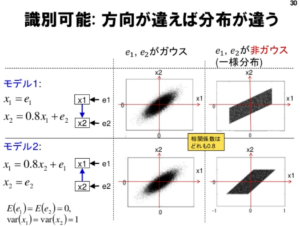
(因果探索: 基本から最近の発展までを概説 P.30)
変数の平均や分散が同じで、正規分布であるとx1かx2どちらがどちらか判断がつきません。
そのため、LiNGAMの誤差項は非正規分布であるという仮定を置いていると読み解けます。
実用時の懸念点
上記に記載した4つの前提で気になる点は複数あります。
(1)Linear
線形な(足し合わせで表現できる)構造方程式で示すことができるとする。
懸念点
本当に因果関係は線形で表せるのか?
例えば、コンビニで購入する経験と行動変容について、下記の条件で行う1回の差は同じだろうか?
・初めて(1回目)の購入(感触:これ良さそう! → 経験:いいなこれ!)
・2回目の購入(これ良かったよね! → やっぱり良いね!)
・3回目の購入(これやっぱり良いよね! → ずっとこれにしよう!)
LiNGAMでは同じと計算されます。
(2)Non-Gaussian
構造方程式の誤差項は非正規(ガウス)分布である。
懸念点
正規分布は、実世界のデータではなかなか見かけないので問題ないのだろうか。特に、購買関係は正規分布は少ない。
実世界のデータで、機器の波形データなどに正規分布があることは周知の事実です。因果グラフ上に正規分布のデータがもし存在した場合は、その変数を除外するのか?正規分布でなくなるように加工するのか?は不明です。
(3)Acyclic
非循環な因果グラフ(Directed Acyclic Graph)で表すことができるとする。
懸念点
一般的に因果は循環しうるのではないか?例えば、購買活動で良い体験が得られた場合は、もう1度経験しようとする動機が生まれるのではないか?
(4)構造方程式でかつ…
未観測の要因が存在しない。
つまり、構造方程式で因果構造全てを表すことが可能であるとする。各誤差項は互いに独立であり、各変数は連続値であるとする。
懸念点
すべての要因を観測できていることはありうるのか?ということですね。無理だと思います。
こちらは。統計的因果推論の傾向スコアマッチングでも問題になりますね。
以上、上記のようにいろいろな疑問点が浮かんできますね。
そのまま推定すると、前提条件から外れているため、因果構造の推定精度が落ちることは予想されます。
その対処には、複数の応用モデルが存在します。
応用モデルおよびPythonモジュールの解説
下記で簡単にインストールが可能です。
pip install lingam
テストコードはLiNGAM – Githubのexampleディレクトリで利用可能です。下記で紹介しているモデルの他にもさまざまなモデルが存在します。
コードの実行については、その他の資料に説明を譲ります。
方法論としてDirectLiNGAMはよく使いそうなので、解説を追加しておきました。
DirectLiNGAM
回帰分析の残差を利用したモデル。通常のICA-LiNGAMより性能が良いとされている。(ビッグデータに基づくモデリング -生体・医療への適用を例として-より)
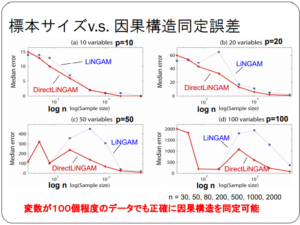
DirectLiNGAM アルゴリズム
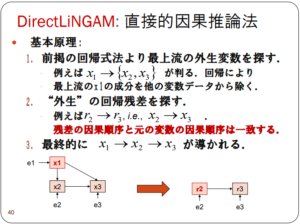
日本語で良い資料がなかったので同資料をコピーしています。
回帰分析を行い、その残差をさらに回帰分析することを繰り返す方法です。意外と簡単ですね。
非線形モデル
関数型を線形→非線形に切り替えます。
巡回モデル
因果を非巡回→巡回に切り替えます。
離散変数モデル
ベイジアンネットワークのように変数を離散変数として扱います。
未観測要因ありモデル(ParceLiNGAM)
外生変数に未観測要因があることを前提に計算します。
離散変数モデル
ベイジアンネットワークのように変数を離散変数として扱います。
時系列モデル(VARLiNGAM、VARMALiNGAM)
時系列(過去・現在)のロジックを追加します。
データ構造変化モデル(LongitudinalLiNGAM)
時間軸でのデータの構造変化を考慮します。
複数データグループモデル(MultiGroupDirectLiNGAM)
複数のデータグループが存在する時、単独でそれぞれLiNGAMを行うより、まとめて行う方がよい精度が出るように考案されたモデル。
以上、その他にも多くのモデルが提唱されていますので、ぜひ試して記事を書いてみてください!
注意点
コードを実際に動かしてみると、実務に簡単に適用できそうと思いました。しかし・・・実務のウラでテストしてみると、実務適用に難しい点が何点も出てきました。
グラフ構造を指定しないと、推定が全くうまくされません
特定のモデルでは、グラフの開始ノードと終了ノードが指定可能です。
ある実データ(売上データ)を使い実験してみました(5例すべて)が、構造を指定しないとうまく予測されませんでした。指定しない場合、一般的と考えられる因果構造と逆、例えばユーザー継続の原因が売上のような結果が出てきました。
データ量が少なすぎると、結果が出力されません
ある実データ(売上データ)で1年間・週ごと(48=4週×12か月)かつ20カラムのデータでは、結果が表示されませんでした。
検証方法がわかりません
カイ二乗検定を使います。つまり、期待値からどれくらい値が外れているか(=有意な差があるか)の指標で判断します。
(因果探索: 基本から最近の発展までを概説 P.37)
ただし、どれくらい値が大きくなれば適合している・していないと言えるのか基準がわかりません。使うとすれば、同じ取得条件のデータで、指標を比較して使うべきでしょう。
SEM(Structural Equation Modeling)との違いが判りません
比較したモデルは、Python LiNGAM(Direct LiNGAM)とSPSS AMOSです。
ある実データ(売上データ)で実験を行いましたが、グラフ構造を指定した場合はほぼ同じ結果(因果の方向、係数の相対的大きさ)が出てきました。ただし、係数の実数値は大きく異なりました。
おまけ:LiNGAMの解き方
1. 独立成分分析(ICA)
DirectLiNGAMと比較してICALiNGAM呼ばれる理由でもある。
2. 復元行列WをAの逆行列から求める
3. ハンガリアン法による最小化
4. 行の順序入れ替え
ICAは行の識別性がないので、入れ替える必要がある。
5. 単位行列Iを除く
6. 因果方向・効果量を特定する
結果. 構造方程式で示すことができる形となる
まとめ
今回は、統計的因果探索のLiNGAMを紹介しました。
「因果構造を把握することで、何をすれば購買につながるのか?」ということは全世界のマーケターをはじめ、購買に関係する社会人は知りたいでしょう。
ただ、実データで利用するとしても問題点があります。
科学的なデータとは違い、そもそもの答えが分からないのです。心理的な背景がどうなっているか、それがどうなるかは私たちの知りうる範囲ではありません。そのため、大規模に実験しづらい問題があります。
なぜなら、時間を掛けて上手く行くかどうかわからないことを試す余力はないからです。何度も何度も実証を重ねて、一般的な因果構造を理解するとどれくらい儲かるのでしょうか?投資対効果が全く分からないのです。
かつ、個人によって因果構造が違うのではないかという懸念もあります。一般的な科学的モデルであれば、因果構造は一定です。経験や環境によってヒトは判断を変えうるのです。それを推定できるのでしょうか?
そのようにいろいろと問題は山積していますが、私はまずは1つやってみなければ始まらないと思っており、データ分析案件実施上の空き時間でテストをしていました。
色々と認識違いがあるかもしれませんが、その際はコメントいただけると幸いです。皆さんもぜひ試してください!
参考文献
発明者の清水さんをはじめ、多くの方の書籍・文献を参考にさせていただきました。
統計的因果探索 (機械学習プロフェッショナルシリーズ)
因果探索: 基本から最近の発展までを概説
LiNGAM: Non-Gaussian methods for estimating causal structures.
つくりながら学ぶ! Pythonによる因果分析 (Compass Booksシリーズ)
etc…
より深く勉強したい方へ
【教材紹介】入門統計的因果推論で因果推論、グラフ理論の基礎を学んでから、清水先生著作の【教材紹介】統計的因果探索を学ぶことでより深い理解が可能です!









[…] 本書と一緒に読むことで理解が捗ります。 統計的因果探索LiNGAM 手法解説 […]