名将と呼ばれた者達のデータを使って、データサイエンスを学んでみましょう!
生きた&整えられたデータは中々公開されていないので、今回の野球ゲームのデータは分析に適していると思われます。もちろん、Kaggle等のデータもありだと思います!
今回やること
野球ゲームの選手について、能力のミートが正規分布であるか(排出設定通りか)確認します。その理由としては、運営の観点から、バグなどの問題がなく、うまく選手が生成できているか?を答えたいと思います。
ゲームデータ(試合結果)
野手データ 20190204.csv
投手データ 20190204.csv
実施内容
はじめに
Jypyter Notebookで分析を進めていきたいと思います。
まずは、コマンドプロンプトを開いて、基本的なパッケージをインポートしておきましょう。
import os, sys, csv import pandas as pd import numpy as np import matplotlib.pyplot as plt
次に、ゲームデータがあるディレクトリ直下まで行って、データを読み込ませておきます。
dfB = pd.read_csv('meisyo_b_20190204.csv', encoding='utf-16')
dfP = pd.read_csv('meisyo_p_20190204.csv', encoding='utf-16')
* 文字化け防止のためcsvはutf-16で出力しています。
データの確認
データの状況把握のためにdf.info()を表示します。
dfB.info() dfP.info()
つづいて、野手(dfB)のデータをメインで見ていきましょう。
Lvのデータをグラフ化しましょう。
plt.hist(dfB['lv'], bins=100) plt.show()
* bins=100にしているのは、Lvが1~100の100分割で設定されているからです。
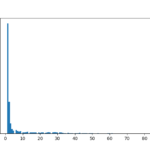
Lv0が多すぎるので、クエリでLv > 10と制限しちゃいます。
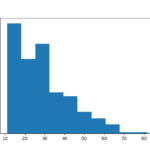
plt.hist(dfB.query('lv > 10')['lv'], bins=10)
plt.show()
dfは「Lv > 10 & Lv <= 100」などSQLみたいに書けるので、応用がいろいろできそうですね。
* 次回以降、plt.show()を省略します。
能力値の確認
それでは、ミート(b_mt)を解析します。
まずはshape(データの行数・列数)とmean(平均値)、std(標準偏差)を表示します。
dfB.shape dfB['b_mt'].mean() dfB['b_mt'].std()
(7893, 96) 32.214493855314835 11.483961920286394
7893データ(n = 7893)、96カラムがありました。これだけでは、ミートがどのようなデータ分布をしているのかいまいちわかりませんね。
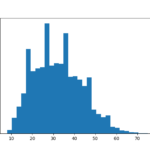
今回は(設定通り)正規分布してるのか?ということが気になるので、b_mtをヒストグラムにしてみます。
plt.hist(dfB['b_mt'], bins=30)
右と左のバランス感から、これは見た限りでは正規分布していないですね。
正規分布の検定
見た限りという主観的な意見ではなく、正規分布であるかどうか判断できる方法論である検定を行います。
正規Q-Qプロット
正規分布の検定によく使われる手法です。こちらは可視化の方法論となります。
import scipy.stats as stats stats.probplot(dfB['b_mt'], dist="norm", plot=plt) plt.show()
直線上に乗ってることが正規分布を示すと考えてください。

低い値の範囲が正規分布していないようですね。
シャピロウィルク検定
他にも正規分布の検定方法はあります。定量化できるので、数値での比較が可能となります。
stats.shapiro(dfB['b_mt'])
C:\Users\saito\AppData\Local\Programs\Python\Python37-32\lib\site-packages\scipy\stats\morestats.py:1653: UserWarning: p-value may not be accurate for N > 5000.
warnings.warn("p-value may not be accurate for N > 5000.")
(0.9833155870437622, 1.85650483425366e-29)
N>5000は正確でないよとアラートが出ていますね。データ量が多すぎたのかもしれません。
結果は、(検定統計量(W), p値)と出力されます。
今回は、p値 < 0.05のため、正規分布であることが棄却(≒正規分布ではない)されています。
歪度と尖度の確認
歪度と尖度が正規分布に近い値か確認します。0になると正規分布ですが・・・
>>> pd.Series(dfB['b_mt']).skew() #歪度 0.364141699620992 >>> pd.Series(dfB['b_mt']).kurtosis() #尖度 -0.3620100293286428
今回は正規分布でないですね。
その他データ加工方法を試す
能力値をある条件下で区切って、正規分布であるかどうかを確認します。
stats.probplot(dfB.query('b_mt > 0 & b_mt < 60')['b_mt'], dist="norm", plot=plt)
他のステータスb_pw(パワー)も見てみましょう。
plt.hist(dfB.query('b_pw >= 10 & b_pw <= 60')['b_pw'], bins=50)
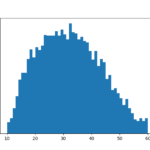
これは・・・ダメかもしれません。左すそは分布が急減していて、右すそは謎の山ができている。
上記を検定してみましょう!
>>> stats.shapiro(dfB['b_pw']) (0.9832108020782471, 1.5380268896554336e-29)
だめですね!正規分布ではない。(‘A`)ンアー
検証結果
正規分布していないという結論になりました。
なぜ正規分布していないかというと3点理由があります。
1・投手と野手では計算式が違うから
2・能力値値が低い選手は削除されるから
3・生成した結果のデータではなく、選手データをそのまま使っているから
1点目については、ミートもパワーも(結果的に打力が)高い投手が出現するなら、野手が要らなくなるよね?それは阻止したい。ということで、「野手能力は野手>投手」、「投手能力は投手>野手」になるように生成の制限をかけています。
それは後述のヒストグラムで確認可能です。
2点目については、ゲームをプレイしているユーザー側の都合ですね。
相対的に弱い選手は淘汰される。ただそれだけです。
そのため、正規Q-Qプロットでミートが低い値の範囲が正規分布していなかったことが予想されます。

3点目については、分析すべき対象データを間違っていたという致命的な内容です。
つまり、今回のデータや分析では何も言えないということです。答えがこれでは出せませんというのが答えという・・・。
さて、頭を切り替えて、野手と投手データを分けると、どう分布してるのか?を見ていきましょう。
plt.hist(dfB.query('type == "P"')['b_mt'], bins=10, alpha=0.3, histtype='stepfilled', color='r') # 投手
plt.hist(dfB.query('type == "B"')['b_mt'], bins=10, alpha=0.3, histtype='stepfilled', color='b') # 野手
plt.hist(dfB['b_mt'], bins=10, alpha=0.3, histtype='stepfilled', color='g') # 全体
ヒストグラムを半透明にして、緑=全体、青=野手、赤=投手で表示しています。
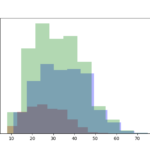
投手と野手の分布が違うことがわかりやすいのではないでしょうか。とはいえ、このように前提知識がないと効果的な洞察は得られません。
野手と投手の分布が違うことをさらに裏付けましょう。
マン・ホイットニーのU検定(中央値の検定)では、投手と野手ではやはり中央値は異なると出ますね。これこそ設定通りですね。
stats.mannwhitneyu(dfB.query('type == "P"')['b_mt'], dfB.query('type == "B"')['b_mt'])
MannwhitneyuResult(statistic=3865093.0, pvalue=4.898308872342808e-180)
加えて、one-way ANOVA(1元配置分散分析)を試します。それぞれの集団が正規分布であることを前提にする検定です。平均値が同じであるかどうか?を分散の違いで検定しています。
よくやりがちなんですが、2群間の検定であるt検定を3群に対してそれぞれ行う(A=B、A=C、B=CだからOK!)という暴挙はしてはなりません。こちらは、統計の適用ミスとして失敗例によく挙げられます。
まずは、3群(全体、野手群、投手群)が正規分布であるかどうかの検定を行います。
>>> stats.shapiro(dfB['b_mt'])
(0.9833155870437622, 1.85650483425366e-29)
>>> stats.shapiro(dfB.query('type == "P"')['b_mt'])
(0.984963059425354, 4.804016817054439e-15)
>>> stats.shapiro(dfB.query('type == "B"')['b_mt'])
(0.9849120378494263, 6.929926115617653e-24)
全然正規分布ではありませんでした。つまり、one-way ANOVAは使っちゃいけない分布です。
続いて、分散分析を行います。(使い方は間違っています)
>>> stats.f_oneway(dfB['b_mt'],dfB.query('type == "P"')['b_mt'],dfB.query('type == "B"')['b_mt'])
F_onewayResult(statistic=447.17232845769377, pvalue=1.25435911612848e-189)
一致するわけがないのでした・・・。
おまけ:追加検証
正規性を検定するシャピロウィルク検定(stats.shapiro())で、標準正規分布を生成するnumpy.random.randn()を検定してみましょう。正規分布を正規分布(正を正)と判断できるかをチェックしています。
>>> for i in range(1, 10):
... temp = np.random.randn(10 ** i)
... print("10^" + str(i) + ":" + str(stats.shapiro(temp)))
...
10^1:(0.9447452425956726, 0.6069143414497375)
10^2:(0.994074285030365, 0.9436165690422058)
10^3:(0.9983760118484497, 0.4763585329055786)
10^4:(0.9998458623886108, 0.7608375549316406)
10^5:(0.9999829530715942, 0.9663644433021545)
10^6:(0.999995768070221, 0.9852367043495178)
10^7:(0.9999997615814209, 1.0)
Traceback (most recent call last):
File "<stdin>", line 3, in <module>
File "C:\Users\saito\AppData\Local\Programs\Python\Python37-32\lib\site-packages\scipy\stats\morestats.py", line 1644, in shapiro
a = zeros(N, 'f')
MemoryError
10^n個の標準正規分布を作らせて検定してみたところ、数が多くなればなるほどp値は1.0に近づきますね。
ただし、統計学では「正規分布していることを棄却できない(=判定を保留している)」だけであって、積極的に「正規分布している」とは言えないことに注意が必要です。
さいごに
今回はゲームデータを用いて正規分布の検定を試してみました。
今回の結論からしても、やはり分析技術の理解とドメイン知識の両輪が必要ですね。
よく読まれるようなら、また別の内容を投稿したいと思います。