今回、会社のコンペで255というとんでもない量の変数を扱うことになりました。
価格予想を行うコンペです。
今回のデータのおさらい
データ量は1500程度。8:2で分けると検証データが300しかないすごく小さいデータです。
1つ1つの変数は「価格(y)との相関関係がほぼない」という特徴を持っていました。
そのうえ欠損値だらけ。穴埋めするだけでタイヘン。
そのため通常行われる下記の1が使えませんでした。
1・変数増加法(前進的選択法、forward selection method)
2・変数減少法(後退的選択法、backward selection method)
3・変数増減法(stepwise forward selection method)
4・変数減増法(stepwise backward selection method)
1番は作ってみたのですが、1変数目から「すべて同じ正答率ですねー」と出て話にならなかった。
それで進めても正答率上がらず・・・。
ランダムに選んでるだけになっていたのでしょうがないか。
というわけで2番を実装しました。
前提条件
すでに前処理を行って、正規化済みの「X」と回答の「y」に分けてあります。
分ける前のデータフレームは「df_a」です。
ある程度実験的に分析してみた結果、一番当てはまりが良さそうなSVRを採用しています。
その他のモデルでも可能だと思います。
※Jupyter Notebook環境を想定しています。
コード
まず初めに、変数選択用のデータフレーム「df_auto_var」と回答の「y_auto」を作成しました。
データをpandasに入れ込んでいる理由は、自動で変数選択を行えるようにするためです。
df_auto_var = pd.DataFrame(data=X, columns=df_a.drop(['sum'], axis=1).columns, index=df_a.drop(['sum'], axis=1).index) y_auto = df_a['sum'].values # yで良かった気がする # モデル選択(チューニング済み) from sklearn.svm import SVR auto_model = SVR(C=50.5, cache_size=200, coef0=0.0, degree=3, epsilon=0.1, gamma=1.0, kernel='poly', max_iter=-1, shrinking=True, tol=0.001, verbose=False) # チューニング済SVR
次に、排除済み変数を入れる「auto_rank」と変数選択リスト「auto_var」を作ります。
あとは、最後に結果表示を行うための「auto_graph」「auto_columns」「auto_data」を作成しておきます。
# 自動用Series(途中保存可能) auto_rank = pd.Series() auto_var = pd.Series(df_a.drop(['sum'], axis=1).columns) # 保存用list auto_graph = [] auto_columns = [] auto_data = []
変数選択リストからカテゴリ変数を外したい場合は、下記のように「auto_var」から当該の変数を抜いておきます。
今回はダミー変数「***_0」では、欠損値であった行は「1」としているのでそれは削除可能にしておきます。
import re
# カテゴリ変数は削除しない(0は自己作成のため削除可能)
for col_var in auto_var:
if re.match(r".*_\d+", col_var) and re.match(r".*_[0]+", col_var) is None:
print(col_var, "Delete")
auto_var = auto_var[auto_var != col_var]
続いて、本命の編集選択プログラムです。
最初はグリッドサーチ(GSCV)入りにしていましたが、
最終的に現コードの「全変数を入れたSVRでグリッドサーチ(ランダムサーチ)を入念に行い、auto_modelに入れて実行する」方法が上手くいきました。
なぜそのようにしたかと言うと、
(1)グリッドサーチを1つ1つ丁寧にできないので上手くいかない
・1変数外すのに255変数全部を検討できない
・1変数ごとに検討しても最低100検討はかかる
「そんなことより他の事をやったほうがいいのでは?」という。変数作成とかね。
(2)自動で丁寧にグリッドサーチすると計算回数(時間)が爆発する、
・グリッドサーチは少なくとも1回5秒かかるので、255変数すべてに行うとそれだけで20分近くかかる。predict等の計算時間も併せて考えると1変数選択で30分以上かかるようになる(上手くいったかどうかも確認できない)
SVRはパラメータによってフィット度合いが全く異なります。
今回の正答率(今回は価格の±10%以内に入ったか)も無チューニング→適当チューニングで15→25%に改善しました。
全然ダメなパラメータが選択されてしまうとその時点での変数選択もうまく行かず、後にも悪影響がありそうです。
というわけで「一番いいやつ」だろうパラメータで試してみて、変数が減ってもそんなに悪影響がなかったのでこの方法を取っています。
※注釈:
グリッドサーチの「scoring」があるので、そこを自己定義関数を使いうまく設定できると良いかも。
グリッドサーチが必要であれば下記を適当にいじってください。
今回は「poly」が上位に来ていたためpolyだけにして計算回数を節約していました。「sigmoid」は低かった。
# GSCV用
cv_param = {
'C': np.linspace(1, 100, 5),
'kernel': ['poly', ' linear', 'rbf', 'sigmoid'],
'degree': np.arange(1, 10, 1),
'gamma': np.linspace(0.1, 1.0, 5)
}
では本命のコードを。
今回はtrain_test_splitのrandom_stateを0にしています。再現性を取るためです。
変数1つ1つを0で埋めて正答率を比較しているだけです。もっと良い方法があるかもしれない。
最後に結果を各listに突っ込んでおくという処理です。
# AUTO_VAR
for i, col_var in enumerate(df_auto_var):
auto_ranks = {}
print('# Rank', i, 'Start.', 'Len:', str(auto_var.shape[0]),'Time:',datetime.today().strftime("%Y%m%d_%H%M"))
# 変数を1残す
if auto_var.shape[0] <= 1:
break
# GSCV前処理
#col_datas = auto_rank.copy()
#X_auto = df_auto_var.drop(col_datas.values, axis=1)
#X_atr, X_ats, y_atr, y_ats = train_test_split(X_auto, y_auto, test_size=0.2, random_state=0)
# GSCV
#SVR_acv = GridSearchCV(SVR(), cv_param, cv=2, return_train_score=False, n_jobs=-1, verbose=2)
#SVR_acv.fit(X_atr, y_atr)
# 特徴選択(Backward Selection)
for col_n, col in enumerate(auto_var):
col_datas = pd.concat([auto_rank, pd.Series([col])])
# X選択
X_auto = df_auto_var.drop(col_datas.values, axis=1)
# 選択されなかった変数は0埋め
X_auto[col] = 0
# TrainSplit
X_atr, X_ats, y_atr, y_ats = train_test_split(X_auto, y_auto, test_size=0.2, random_state=0)
# Fit
auto_model.fit(X_atr, y_atr)
# Check
auto_acc = 0
auto_pred = auto_model.predict(X_ats)
#auto_pred = SVR_acv.best_estimator_.predict(X_ats)
for j, n in enumerate(y_ats):
acc_per = (auto_pred[j] - n) / n
if abs(acc_per) <= 0.1:
auto_acc += 1
auto_ranks[col] = auto_acc / y_ats.shape[0]
print(" (%s/%s) %.2f% [%s]" % (str(col_n).zfill(3), str(auto_var.shape[0]).zfill(3), auto_ranks[col]*100, col))
# ソートして点数順(昇順)にソート
auto_ranks_sort = sorted(auto_ranks.items(), key=lambda x:x[1])
auto_result = [k for k, val in auto_ranks_sort[:]]
# dropカラムに入れる
auto_rank = pd.concat([auto_rank, pd.Series(auto_result[-1])])
auto_var = auto_var[auto_var != auto_result[-1]]
# グラフに追加
auto_columns.append(auto_result[-1])
auto_graph.append(auto_ranks[auto_result[-1]])
auto_data.append(auto_var)
print("→ [%s] %.2f%" % (auto_result[-1], auto_ranks[auto_result[-1]]*100))
工夫した点としては以下の4点。
(1)処理を中断しても途中から再開できる(カーネルが死ななければ、ですが)
(2)時間を先頭に書いているので、変数選択がだいたいどれくらいで終わるのか予想できる
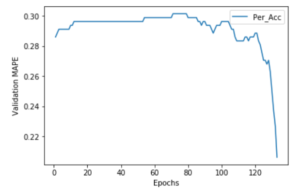
(3)結果の推移をグラフ「auto_graph」(後述)で見れる
(4)良さそうな変数設定を「auto_data」から引っ張れる
特に(4)が良いです。
変数選択したけれど「結局どんなカラムでやればいいの?」という答えに即答できますね。
データを一々見るのは面倒ですよね。
あとは結果の表示と、
# プロット
plt.plot(range(1, len(auto_graph) + 1), auto_graph, label="Per_Acc")
plt.xlabel('Epochs')
plt.ylabel('Validation MAPE')
plt.legend()
plt.show()
どんな順番で変数が抜かれたかを書いておきます。
for i, col in enumerate(auto_columns):
print(str(i).zfill(3), math.floor(auto_graph[i]*10000)/100, col)
最後に、正答率が一番が良かった結果を表示します。
arg_max = int(np.argmax(auto_graph))
print('No.', arg_max, 'Per:', auto_graph[arg_max])
print('Columns:', auto_data[arg_max])
まとめ
今回は変数選択法の変数減少法(後退的選択法、backward selection method)を少々無理やり実装しました。ある程度変数の数が少なければ、手動で選択をかけても良いと思います。(意味のある変数が多ければ!)
手作業でちょこちょこやるのは時間あるときはいいのですが、これだけ多いと無理があります。変数作成や問題に合いそうなモデルの選択、グリッドサーチ等、精度に直結することに時間を掛けたいものですね!







[…] 。前進的選択法は変数が残念すぎて「どれも同じですねー」としか出なかったので却下。(詳細) →だいたいこれで変数が40個くらいになる。 変数合成・・・これから作る予定。元々あ […]