データ分析業務ははっきり言って泥臭い。
分析の設計を行い、可視化を行ってから使えるデータかどうか判断できる。
そもそもそれはデータ分析前の話なのだが。
今回は、可視化の中でもデータの傾向を把握するのに役立つヒストグラム、その階級数を決める方法論を確認したい。
そこには思わぬ落とし穴があった。
1. きっかけ
筆者はコンサル(自社)やデータ分析受託会社、事業会社への研修を行うことが度々ある。
統計学をはじめ、科学は一つ一つの積み重ねで結果を出す。
そのうち、1ステップでも間違いがあれば結論が覆ることがある。
初学者はよく間違いを犯す。私もそうだった。
~その昔~
上長「決定木で要因分析した後、分かれたノードごとに数値を確認しておいて。」
ワイ「平均値と標準偏差が一致することを確認しました!問題ないです!」
上長「おっ早いね。分布はどうだった?」
ワイ(あ、分布は見てなかったわ・・)
ワイ「データはあるので今可視化しますね~」
ワイ「なんやこれ・・・全然違うやんけ」
上長「せやな」(やり直して来いよー)
ここまではっきり出ることは珍しいが、よくありがちなミスである。
要因分析をしたところで、ユーザー層が全く違う人たちを取ってくることはままある。
ユーザー層が似通っている根拠づけとして、分布を確認することは必要だろう。
データ分析の前段階で良く行うのは、平均値や中央値、標準偏差など代表値を確認することである。
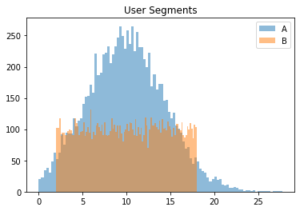
ただし、今回のように当たり前に使われている代表値が意味をなさないことがある。
ちなみに、上記の平均値と分散は、どちらも10、4.5あたりである。
(実験コード(1)は後に記載している。)
可視化しない場合はほぼ変わらないと判断されてもおかしくはないだろう。
今回可視化したことによって、判断が変わることだろう。
2. ビン数決定どうしよう…
そういった背景もあり、基本的に私は必ず分布を確認することにしている。
ただ、分布を確認する場合、どうしても越えなければならない壁がある。
階級数設定(ビン付け)が経験則になることである。
それに対して、最近統計学入門(基礎統計学Ⅰ;赤本)を読み返していたところ、可視化のうち、ヒストグラムに関する記載があった。
P.22
このように、ヒストグラムを描くことによって、現象の基礎にある本質が発見されることがあり、単に理解の手助けとなるだけではないことが分かる。
同
度数分布表やヒストグラムを作成するときに注意すべき点は、階級数の問題と階級幅の問題である。
(略)
このように、階級をどのように取るかを決める統一的ルールはない。
うーん確かになあ。
例題として挙げるなら、以下のような分布があったらどうするかという話が一般的だろうか。
まずはそのままビン数は10。

正規分布かな・・・?170という数字に意味があるのかな。
次にもう少し細かくしてみる。k(ビン数)=100だ!
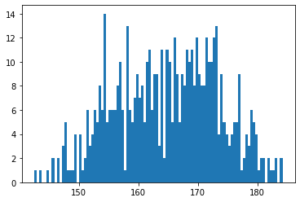
なんだろう・・・細かすぎてよくわからない。
ここで正解を出しておこう。
これは、30代の日本人男女の身長(cm)の分布を合わせたものである。
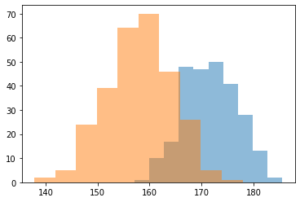
データは国民健康・栄養調査 身長・体重の平均値及び標準偏差 – 年齢階級、身長・体重別、人数、平均値、標準偏差 – 男性・女性、1歳以上〔体重は妊婦除外〕 を利用した。
簡単な多峰性を持つ正規分布だということは答えを見たらわかるが、ヒストグラムを描写しているときはイマイチわからなかったのではないか。
この正解の図を簡単に出せるとありがたいのだが。
赤本によると、スタージェスの公式というものがあるらしい。
k ≒ 1+log2(n)
*k=階級数の目安
*n=サンプルサイズ
ふむ、使ってみよう。今回は10になるのか。これって最初に確認したような・・・

やっぱりわからねえええええええ。。。。。。
答えが分かっているから何となくそれっぽく見えるが、前情報がないと判断できないだろう。
前情報が分からないから判断は難しいのである。
よし!それなら総当たりや!
for i in np.arange(10, 100):
print("i=%s" % i)
plt.hist(y, bins=i)
plt.show()
1つずつ見たけど、なんもわからん・・・という人が多いのではないか。
それっぽく見えるけど、決定的な証拠として採用できるものがない。
作成したy1, y2のデータは、コード(2)の通りである。
y1 = np.random.normal(loc=171.2, scale=5.5, size=257) y2 = np.random.normal(loc=158.6, scale=6.0, size=282)
「これならわかりそうなもんだけどなあ・・・」
私も思った。でもわからないのだ。
このように、分布を確認したほうが良いが、したところで何かが分かるとは限らないことに注意が必要だ。
ヒストグラムの階級数を決める方法論は・・・今のところなさそうだ。
今回のように多峰性があり、かつ分布が2つのみであることが事前に分かっているのであれば何らかの方法は取れるかもしれない。
しかし、ビン付けの総当たりをしてみたが、有効そうな数値は存在しなかった。
そのため、どのような数値を計算式で求めたところで意味がないと判断した。
*この判断も経験則であるが、ヒトのイメージでの判断能力は意外と高い。画像認識も然りだ。
実験コード
(1)
import numpy as np
import matplotlib.pyplot as plt
n = 10000
# 一様分布用関数
def randint(a, b, n):
return (b - a) * np.random.rand(n) + a
# 正規分布
y1 = np.random.normal(loc=10.0, scale=4.5, size=n)
y1 = np.where(y1 < 0, np.nan, y1)
y1 = y1[~np.isnan(y1)]
# 一様分布
y2 = randint(2, 18, n)
y2 = np.where(y2 < 0, 0, y2)
y2 = y2[~np.isnan(y2)]
# 可視化
plt.hist(y1, bins=100, alpha=0.5, label='A')
plt.hist(y2, bins=100, alpha=0.5, label='B')
plt.title('User Segments')
plt.legend()
plt.show()
# 代表値計算
print("A:", np.mean(y1), np.std(y1))
print("B:", np.mean(y2), np.std(y2))
(2)
y1 = np.random.normal(loc=171.2, scale=5.5, size=257)
y2 = np.random.normal(loc=158.6, scale=6.0, size=282)
y = np.append(y1, y2)
# 問題提起
plt.hist(y)
plt.show()
# ビン100
plt.hist(y, bins=100)
plt.show()
# 正解
plt.hist(y1, alpha=0.5)
plt.hist(y2, alpha=0.5)
plt.show()
# スタージェスの公式
def calc_sta(n):
return int(1 + np.log2(n))
plt.hist(y, bins=calc_sta(len(y)))
plt.show()
print(calc_sta(len(y)))
# 総当たり
for i in np.arange(10, 100):
print("i=%s" % i)
plt.hist(y, bins=i)
plt.show()