[Meisyo]練習難易度の不均衡是正への分析的アプローチ

「練習ごとに難易度が違いすぎるんですけど！！」という不満は把握しています。
ただ、これまでそこには触れてきませんでした。

なぜなら・・・まだデータ取れてないし、分析できないでしょ（言い訳）

・・・怠慢デスネ！

とりあえず大枠でざっくりと分析します。

分析を行うデータの期間

データ取得開始～2019/02/28

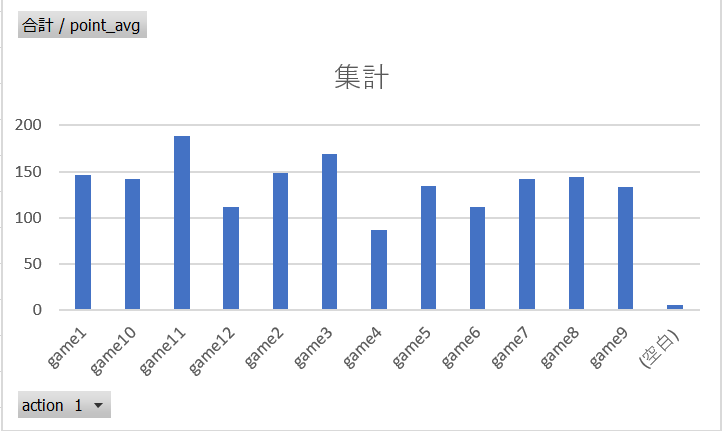
練習全体の分析

sub	action  1	point_avg	point_stddev
practice		5	26
practice	game1	146	53
practice	game10	142	45
practice	game11	189	35
practice	game12	112	55
practice	game2	148	39
practice	game3	169	53
practice	game4	87	38
practice	game5	134	53
practice	game6	112	55
practice	game7	142	41
practice	game8	144	59
practice	game9	133	35

すると、game4が難しくて、game11が簡単なのでは？という疑問が生まれてきます。

game4

game11

「あっ・・・確かに。」とプレイしている身からは腹落ちします。
だってgame4で200ポイント＝5ビンゴしないもん。無理。
game11は簡単すぎて笑えないし。

コードは以下の通り。

SELECT
	sub
    , SUBSTRING_INDEX(action, ',', 1) AS action
    , CEIL(AVG(SUBSTRING_INDEX(action, ',', -1))) AS point_avg
		, CEIL(STDDEV(SUBSTRING_INDEX(action, ',', -1))) AS point_stddev
FROM
	acts
WHERE
	sub = 'practice'
	AND time < '2019-03-01 00:00:00'
GROUP BY
	SUBSTRING_INDEX(action, ',', 1)
ORDER BY
	action;

各々の練習の分析

今回の分析の目的は、「練習の得点をだいたい150%平均くらいにしたい」にします。
目的が決まっていないと、分析したけど「で？どうすんの？」という話なので。

分析方法

下記の流れで進めます。
1・分布の確認。（現状把握）
2・目的達成へのアプローチを考える。（仮説設定）
3・分布の推移を見る。（効果検証）次回以降

このように、現状把握→仮説設定→検証→・・・の流れで進めます。
まあいたって普通な流れですね。

game1

ゲーム：ストップウォッチで*秒で止める。

集計データ：
　平均：146
　標準偏差SD：53
　「とりあえず目標は達成してるんじゃないかな？」と思います。

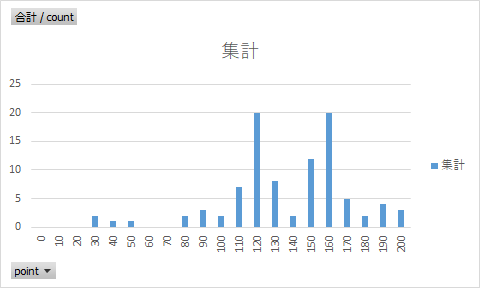
分布：

集計データから一転、「正規分布とは一体どこへ・・・」みたいな分布になっています。

「得点が正規分布する＝ユーザーは成長しない」という前提に立っていることに注意してください。

「十分にプレイした後（＝伸びしろがない状態）で集計する」なら正規分布するであろうと。
考えられる仮説としては、「最初はユーザーが慣れていなかったが、慣れたら簡単だった」という。
ならユーザー毎の時系列での成長傾向を調べようってなりますね。

＼そもそも数が少ない／
数が少ないと継時変化のデータの取りようがない。

コードとデータは以下の通り。
データ：
　meisyo_acts_20190303.sql
　SQLです。PHP MyAdmin等に即インポートできます。（ゴミデータも混じってるので扱いには注意が必要）
　SEQというseqカラムに0～999まで入れたテーブルを別途作成してください。

コード：
21行目の「game1」を変更すれば、全練習に対応可能です。

SELECT
	SEQ.seq as point
	, COALESCE(ACT.count, 0) as count
FROM
	(SELECT
		(seq * 10) AS seq
	FROM
		an_seq
	WHERE
		seq BETWEEN 0 AND 20) AS SEQ
LEFT JOIN
	(SELECT
		SUBSTRING_INDEX(action, ',', 1) AS act
		, CEIL(SUBSTRING_INDEX(action, ',', -1)/10)*10 AS point
		, count(*) AS count
	FROM
		acts
	WHERE
		sub = 'practice'
		AND time < '2019-03-01 00:00:00'
		AND SUBSTRING_INDEX(action, ',', 1) = 'game1'
	GROUP BY
		act, point
	ORDER BY
		act, point) AS ACT
ON SEQ.seq = ACT.point
ORDER BY
	SEQ.seq
;

実施内容：
　とりあえず150点くらい取れるので、game1は何もしません。

game2

ゲーム：任意の桁数の数値を打ち込む

集計データ：
　平均：148
　標準偏差SD：39
　とりあえず150近くだし問題ないよね

分布：

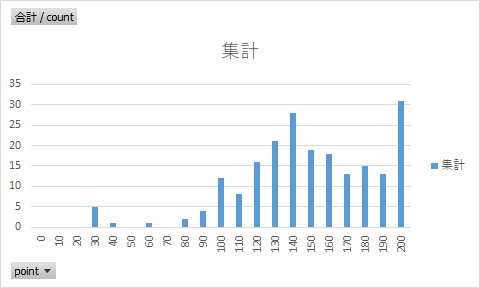
200が多いのが気になる。30もあるのか・・・。
ただし、平均が140あたりで正規分布の山を作っていると仮定すると、
真の200が15、210が10、220が5（合計30）と予想できるので、それが200に積まれている・・・のかな？
問題なさそうですね。

実施内容：
　何もしなくてOK。

game3

ゲーム：指定された順番に文字をクリックしていく

集計データ：
　平均：169
　標準偏差SD：53
　ちょっと高いような気がするので、下方修正を掛けたい

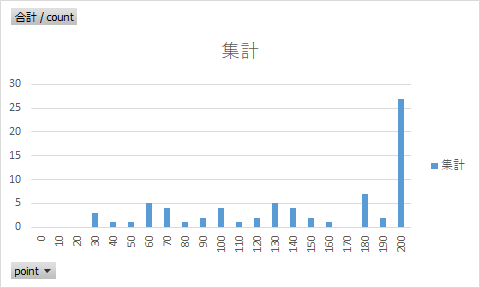
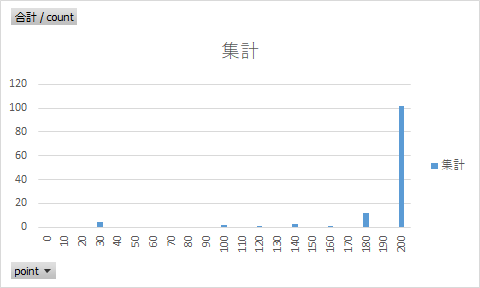
分布：

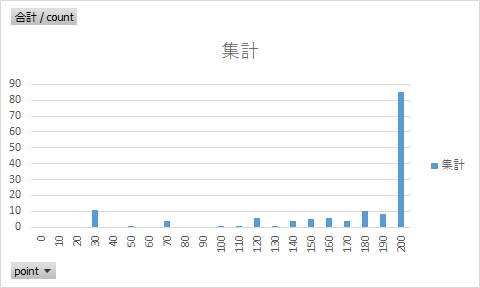
簡単すぎたワロタ・・・
集計データと全然印象が違いますね。

現在は1数字＝0.8秒で計算しているので、それを調整します。
では、何秒にすればいいのか？

ちょっとよくわからないですが計算してみます。（正しいかどうかは置いといて）
現在は147回中、得点が200に85回（57.8%）集中しているので、
真の中心は200より右にあることが想定できる。
加えて、グラフの通りこの分布は一様分布（各得点の分布が同じくらい）であることを仮定できる。
一様分布のため、真の200が10程度（6.8%）とすると、210以降に分布する確率は50%となる。
そのため、平均値は200～210の間になる。
現在の1数字あたり0.8秒であると、平均値は200～210（205とする）。
1数字あたり0秒とすると、平均値は0になる。（そりゃそうだ。実際は最低補正25が入るんだけども。）
数字あたりの秒数が平均値と正比例すると仮定すると、係数は「256.25 * 秒」となる。
この値が150程度になってほしいので、
256.25 * 秒 = 150
ゆえに、秒＝0.585

実施内容：
　1打＝0.585秒に修正する。
　結構無理やりな気がする。ただ効果の検証を行えれば、この仮定（数字あたりの秒数が平均値と正比例する）が正しいか確認できる。
　で、200から下に分布の中心が来たら、正規分布等々の推定ができる。
　今はどっちもわからないので、とりあえず試そう。

game4

ゲーム：スロットマシン。すべての数字を一致させたい。（願望）

集計データ：
　平均：87
　標準偏差SD：38
　とりあえずヤバい（語彙力）
　ちなみに得点最下位なので、てこ入れは必須ですね。

分布：

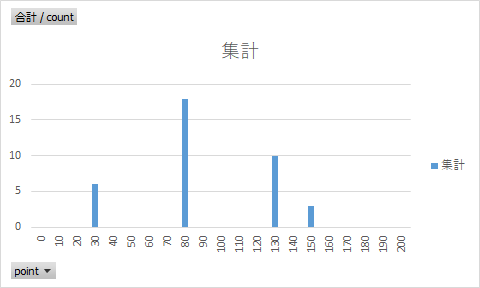
意外とまともな分布かもしれない。平均値は置いといて。
200も一応存在するんですが、誰一人として到達しませんでした！

条件：
・数字は1～15。
・スロットの数は5個。
・得点(ビンゴ数)は、25(0),75(1),125(2),150(3),200(4)の通り。
・各スロットの速度（更新速度（ms））は、120,100,80,65,50。

合計試行回数37って少なくない・・・？他は200まで行っているものがあるのに。
毛嫌いしてるんでしょうか。僕もコレ嫌いです。

ビンゴ3個（X-X-X-X-n）で約8%。
場合分けで考えられないのが厳しい・・・。
なぜなら、それぞれのスロットの速度が異なるから、目押し成功率との相関係数を仮定しないと計算できないため。
更新速度が早ければ早いほど、狙う数値（±0）からの誤差が大きくなって分布の形が平べったくなっていく。

-2:|
-1:|||||
±0:|||||||||||||||||||
+1:|||||
+2:|

↓　速度が早いと・・・

-2:||||
-1:||||||
±0:|||||||||
+1:||||||
+2:||||

ということで、更新速度をすべて統一し、100msとします。
もし、反応速度が200±10msならば、狙っていさえすれば1回86.2%程度の確率で当たる。
（0～100msを10msごと（10個）に分け、正規分布をとるとすると、片側検定の考え方で、(4*100+2*97.5+2*83.5+2*50.0)/1000=0.862）

で、面倒なこととしては、スロットで外れた値も当たり値としてカウントが可能なところ・・・と思っていたら、そんなことはなかった。
一番左の数に当たっているか？当たっていたらその数値が最優先される。
つまり、「15」「1」「15」「1」「1」でも2HITになる。

4回当てる可能性は・・・0.862^4 = 55.2%
（ん？これで計算合ってるの？）

ちなみに、ヒトの光刺激に対するボタン押し反応の速度は209ms（SD：10）（反応時 間研究の歴史と現状）だそうです。集団で反応速度を計測しており、個人として平均±SDを出しているわけではないので本当は参考にしてはならない。

実施内容：
　更新速度をすべて統一し、100msとします。とりあえず。

game5

ゲーム：落ちてくるボールをタイミングよく中心でキャッチする。

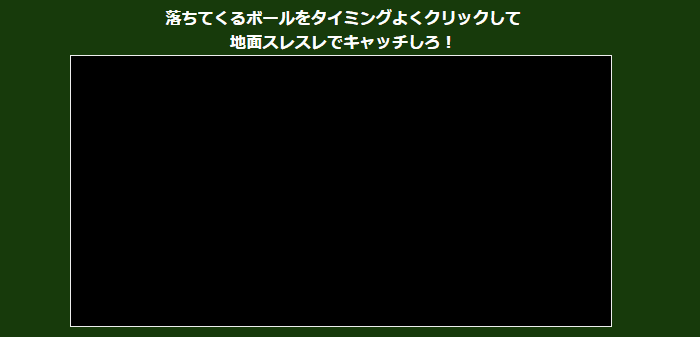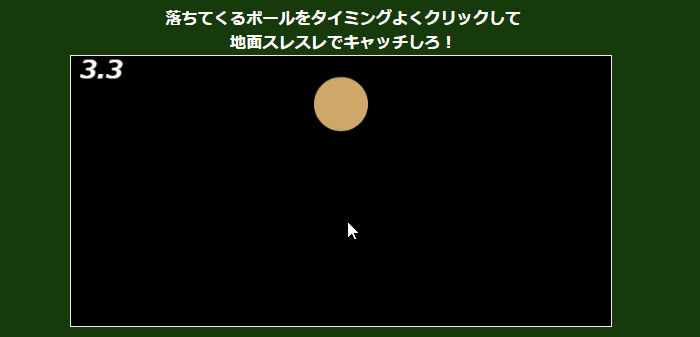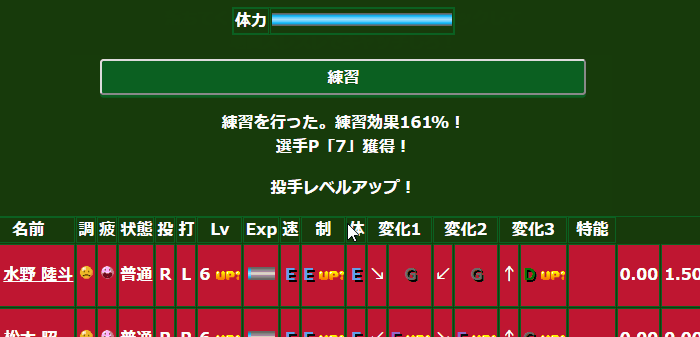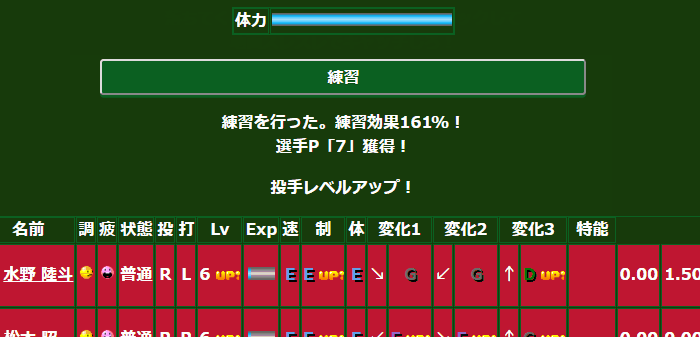
集計データ：
　平均：134
　標準偏差SD：53
　少し（10%）低いような気がします。

分布：

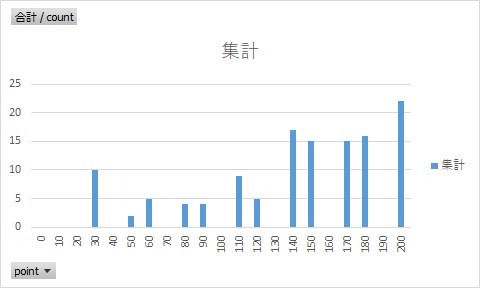
何とも言えないのですが・・・。
分布もまあまあ悪く・・・ないのか？何と言えばいいのかわからない。

ポイントの計算式は、goal（誤差ms）に-300を掛けるというおおざっぱなモノです。
myGame = -300 * Math.abs(goal) + 200;

平均134ということは、-66 = -300*(goal)
AVE(goal) = 0.22s
goal係数 * NEXT = -50にしたいので、
goal係数 = -227

実施内容：
　goal係数を-227にします。

game6

ゲーム：落ちてくるボールをタイミングよく中心でキャッチする。（縮尺変更、距離変更あり。）

集計データ：
　平均：112
　標準偏差SD：55
　ん～・・・正規分布なら、標本内の20%程度しか150を超えていない。
　上方修正が必要そうですね。

分布：

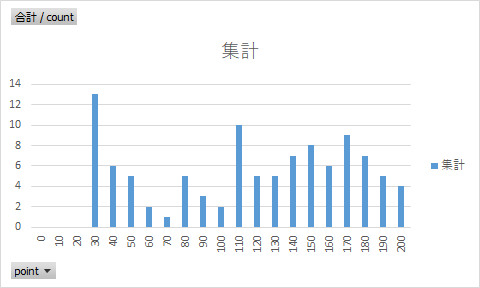
結構25が多そうやな？
縮尺（落ちる距離）がランダムで変化するので、プレイしてる側からしてもちょっと対応が難しいかもしれません。
チリみたいなのがたまに出るので・・・アレほぼ見えないです。

データ数が少ない！！
あとランダム性があるので、それをすべてまとめて分析しても因果関係が不明。

困った・・・。
というわけでgame5と同じことをします。（安直）

実施内容：
　goal係数を-227にします。

game7

ゲーム：振り子2つを中心に合わせられるようクリックする。

集計データ：
　平均：142
　標準偏差SD：41
　とりあえず平均的だしいいよね。

分布：

ああ・・・なんだかとってもいい分布（錯乱）
割ときれいに分布しており、平均値もぼちぼちいい感じなので、
とりあえずこのままで。

実施内容：
　何もしません。

game8

ゲーム：ちょっとだけ違う色（濃淡）を判定する。

集計データ：
　平均：144
　標準偏差SD：59
　これもまずまず。変更しなくていいかも。

分布：

200多くない・・・多くない？（37.5%）

感想としては、そんなに早く見分けつくかなあと思いました。
携帯とかだと特にわからん気がするんだが。（色識別は苦手かもしれない）

何とも言えないのでこのまま置いときます。

実施内容：
　何もしない。

game9

ゲーム：色のついたタイルを高速でクリックする。

集計データ：
　平均：133
　標準偏差SD：35
　少し(10%)上方修正すべきかな？

分布：

正規分布してそうだけども・・・。

ゲームとしては正解1個辺り8Pずつたまっていく。
10秒で終了。
200P＝25回って0.4sに1回正解するのか。すげえな・・・。

120と160が高い理由としては、もしかして8P（10Pではない）に関わるのでは？
得点は、80, 88, 96, 104, 112, 120, 128, 136, 144, 152, 160, 168, 176, 184, 192, 200を取る。
やはり・・・120と160に割り振られる値は2個ありますね。（144が欠損してそう）
そうして見ると、山がちょうど150になってそう。
何もしなくていいかなと思いました。

実施内容：
　何もしません。

game10

ゲーム：わしが考えた最強のマインスイーパーもどき。（クリックするとゴールまでの距離が出る。）

集計データ：
　平均：142
　標準偏差SD：45
　大丈夫だ。問題ない。

分布：

まあ良さそう。

これは得点(正解までの手数)を25(5~),50(4),100(3),150(2),200(1)を取ります。
分布としてもまあまあ合格点だと思います。
意外と頭使うのと、運要素が大きいかも。

これを機械に探索させると面白そうですね。

実施内容：
　何もしません。

game11

ゲーム：他と違う数のパネルをクリックしていく。

集計データ：
　平均：189
　標準偏差SD：35
　簡単すぎぃ！

分布：

簡単すぎぃ！

ということで、ゲームの基礎情報のおさらい。
ゲーム時間：15s
ポイント：1回正解で20p
・・・たった10回正解すればいいのに、15sもあるの？
game9は0.4sに1回（10s、1回8p）なのでそれと同等にしよう。
（あっちは色判別だけなのに、こっちは文字識別が必要・・・だぞ？）

実施内容：
　ゲーム時間：15s→10s
　ポイント：20p→10p

game12

ゲーム：反応速度ゲー

集計データ：
　平均：112
　標準偏差SD：55
　ちょっと上方修正必要では・・・

分布：

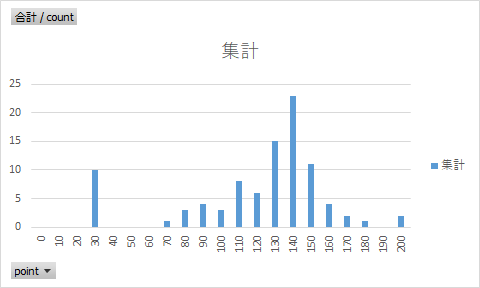
悪くはないけど、ちょっとシビアかなあ。
左裾が伸びている。（だからどうした）
まあミスしてる人も多いのでこんな感じかと。

得点は以下の数式で与えられる。
myGame = (0.8 – Math.abs(myTime)/1000) / 0.7 * 200
反応が0.1s以内なら200点以上・・・って。
いやちょっと待て。人間の限界は0.15sくらいのはず。FPSの上手い人でもその程度だった気がする。
計算すると平均112が反応速度0.40s・・・？

この前提から考えて、式を変更してみる。
myGame = (0.8 – Math.abs(myTime)/1000) / 0.7 * 200
↓
myGame = (0.9 – Math.abs(myTime)/1000) / 0.7 * 200
これでだいたい平均が142になるはず。

実施内容：
　（得点の変更）myGame = (0.9 – Math.abs(myTime)/1000) / 0.7 * 200

まとめ

game1～12までのデータを分析し、練習難易度の不均衡是正を目指しました。
とりあえずこの内容を今日から施行し、1か月後（4/1ごろ）に3/4～4/1のデータを分析したいと思います。

因果関係がわからないランダム要素を入れてしまうと、詳細な分析ができない・・・。
これは新たな発見でした。