これは何?
某社で行われている社内コンペのメモです。私の備忘録でもあります。
結果:1問差で2位でした。残念。
今回の目的変数
建築物の坪単価
※「え、建物の単価じゃないのか」と思ったあなたは正常。
今回の評価指標・ベースレート
正解単価の±10%以内に入った数 / 全数
※35%を超えれば良い(2019/09/19 やっと超えました。)
※重回帰(LinearRegression)でのベースレートは22%
今回の説明変数の特徴
0. リアルデータで欠損値が多い。
打ち込みミスが多く、データの信頼性が低いかもしれない(担当者談)←マジカヨ・・・
確かに延床面積と建築面積が同じっておかしいよなあ!10階~の建物なのに。(なお、その補正はしてないもよう。)
1. どれが一番重要という変数がない。
自作合成変数(Nullカラム数が多いと坪単価が低い)が変数重要度No.1だったりする。
2. 変数の数が多い
138変数ある。
カテゴリ変数をone-hot化するだけで255変数!
3. 決定木の場合はone-hot化すると判定精度が低下しかねない。
線形の場合は必須。
線形と決定木系のよくやる前処理方法は違うようだ。アルゴリズムが全く別だししゃーないか。
4. 設計会社区分で各カラムのmean、medianを取ったがうまくいかず。
上記の方法は、Train内で情報リーク(TestにTrainの情報が行って判別精度を甘めに見積もってしまうこと)が起こってしまうので採用できないようだ。
上記区分が不均一なデータだったので、SMOTEを試したがうまく行かず。
そもそもSMOTEはあまりうまく行かないようだ。(まあ適当にN点間の平均値取ってるだけだし仕方ないよね。)
5. 専門知識が無い
カラム内容を見てもさっぱりでした。もちろん少しは本で理解したが。
今回の目標
基本に忠実に行う。
コードはできるだけ自動化させる。(変数選択、合成等)
目視で変数選択しようにも、重要度がどれもほぼ変わらないぞ~(==;)みたいな状態だったので。
基本(的な学習器)に忠実に(テストして、最高のモノで学習を)行う。
回帰の場合は下記の通りとなっているが、果たしてそうなのか?
SGD
↓
L1 ElasticNet
↓
L2 SVR(linear)
↓
SVR(rbf) EnsembleRegressors
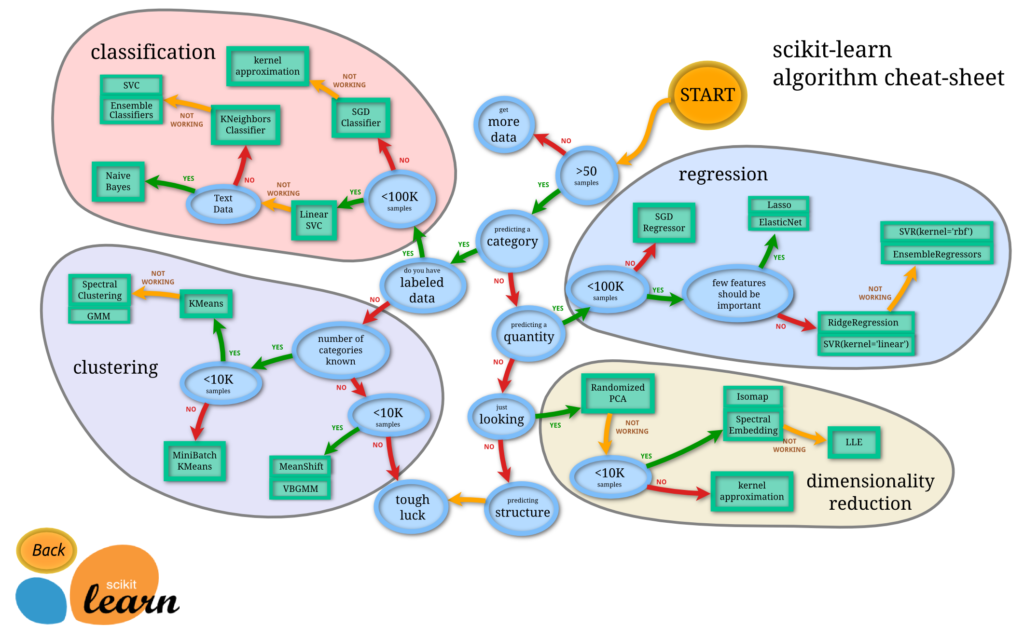
Choosing the right estimator – scikit-learnより
作った処理の流れ
注意するところ
最適なCV方法をまず見つけることが一番大事。正答率という羅針盤がない航海になる。
変数名が専門用語だったので理解できず。業務内容理解しよね。
内容確認
Train+Testまとめて実施した。平均値埋めとかしない限りはリークは起こらないので問題なし。
目的変数を加工してはいかんのか?
→ いかんわけじゃない。目的変数を正規化したり、log化したり、合成するのもありだったりするようだ。
データ可視化
ひと目見て、あっ・・・(察し)となった。
目的変数に大きな外れ値が存在した。
それで何も考えずに行った正答率が非常に低かったのかも。
IQR(四分位値のアレ)を使って除外した。
説明変数にも大きな外れ値(カテゴリ変数はもちろん除く)があったので、
IQRを使ってNull化→欠損値と違う値で埋めた(決定木用)。これは精度向上に効果があった。
加えて、色々切り分けて見ても重要な変数がほぼない。
設計会社区分別での坪単価等が異なったので、それらしい変数を入れてみたがうまくいかず。
相関係数確認
-0.5~0.5だらけ
欠損値補正
Median、0等で埋めたり、TrainのみAveで埋めたりした中で一番良いやつを頼む。(ただし情報リークには気をつけることだ。)
学習器を使って埋める方法等もっとあると思う。
ただし、Mean埋めは線形タイプに、0(や-1など元々のカラム出てきてない値)は決定木タイプで使用するとGood。
異常値であることを機械に知らせてあげよう。
Nan値を予測して埋める手法を試してみたが正答率は結局下がった。もしかしたら線形タイプでは上がるかもしれない。
もう少し工夫はできる気がする。
変数合成
Null個数カラム=「レコードの中にNull値数が多いレコードは何故か値が低い」という知見を利用。
データ水増し
今回はやりましたがうまくいきませんでした。
分類(特に画像処理)だとよくやるもよう・・・画像を回転させるとそれだけで1枚にできるらしい。
正規化
MinMax、StandardScaler、RobustScaler、Normalizer
今回はMinMaxが一番良かった。StandardScalerが死んでた。
ただし、線形には効果はあるけど、決定木系には効果なし。
決定木系は順序(Rank)と集合で見ているもよう。
多モデルのテスト
テスト用関数も作った。
一番いいやつを頼む。
線形
from sklearn.linear_model import LinearRegression # 重回帰分析 LR = LinearRegression() from sklearn.linear_model import SGDRegressor # データ量多い回帰 SGDR = SGDRegressor() from sklearn.linear_model import Lasso # ラッソ(L1) L1R = Lasso() from sklearn.linear_model import Ridge # リッジ(L2) L2R = Ridge() from sklearn.svm import SVR # サポートベクター回帰 SVRR = SVR(gamma='auto')
決定木
from sklearn.tree import DecisionTreeRegressor # 決定木 DTR = DecisionTreeRegressor() from sklearn.ensemble import BaggingRegressor # バギング回帰 BGR = BaggingRegressor(DTR, n_estimators=10, max_samples=0.3) from sklearn.ensemble import RandomForestRegressor # ランダムフォレスト回帰 RFR = RandomForestRegressor(n_estimators=100) import xgboost as xgb # XGB XGBR = xgb.XGBRegressor(objective="reg:linear")
厳密に言うとバギング回帰は決定木ではない。
今回は中に決定木を入れているので決定木にした。
結果
XGBの独り勝ち
価格予想の論文でSVRが使われていたので、コレで頑張って22 → 40%くらい出してた。(つもりになっていた。ただの過学習だった)
しかし、XGB(回帰)をちょっと入れてみるか・・・結果33%で「は?(これまでの頑張りとは)」ってなった。
基本に忠実にやってみたけどやっぱりXGBが強い。
SVRも結構できる子やな~って感じ。(ただし過学習の恐怖からは逃れられない。)
CV値(自作関数)の確認も行った。
決定木の前処理を行えば、線形は死んで(マイナス突破)いた。
決定木系はプラスだった、が正答率25~30%程度と低い。
パラメーターチューニング
グリッドサーチ
・SVR、XGBで頑張った。
SVRは結局kernelはpolyが一番良く、sigmoidが一番悪かった。変数減らしてやったほうがとても早い。
ランダムサーチ
・SVR、XGBで頑張った。
今回評価指標がすごくレアなものなので、グリッドサーチに勝てなかった。過学習してるだけかも知らん。
その他の学習器の試行
keras(MLPとNNとDeepLearning)
Train+TestのdropNA後標準化のみ(8変数)で32%が出たように見えたが、変数が増えると死んだ(20~25%)。
たぶん変数の多さに比べてネットワークの大きさが足りない(層を多くしたりノードを横に増やすとプラスだったが限定的だった)。
あとは前処理が全然試行錯誤できていない。Log処理(疑似標準化)が強いもよう。
変数自動合成
元々あった255変数を、下記の方法で正答率が上がるものをピックアップして追加する。
・組み合わせ(+、-、×、÷)
・変数単独で計算(x^2、exp、log2、log10)する
ただし、めっちゃ手間がかかるので遺伝的プログラミング(遺伝的プログラミングによる特徴量生成でLightGBMの精度向上【kaggle Advent Calendar 11日目】)を導入した。コードはコンペが終わったら全部載せました。↓下の方にあります。
決定木は変数間の相互作用的なのは見えやすいが、比率(割り算)や差(引き算)を認識するのが困難なのでこういった自動化の手法は必須だと考えている。
3つ以上の変数の合成変数もアリなもよう。(遺伝的プログラミングなら理論上試行する)
変数選択
今回は後退的選択法を選択。
チューニングしたXGBを使い、重要度の低い変数から1つずつ削り取っていく方法にした。(詳細)
変数の重要度が低い順から「切ったら精度下がるか?」で判定する方法を実装している。(自作)
回答提出用加工
下記の方法を採用
・なにもしない単一モデル
・平均アンサンブル
・重み付けアンサンブル
Aveや価格帯での重み付け(「ここら辺の価格帯はこの学習器が調子いい」というのがあるので)で具合のいいように組み合わせてみる。
分類は多数決が多いらしい。
回帰でアンサンブルって聞いたことがない(たぶん不勉強→Aveアンサンブルが多いもよう)。
平均が残念だったので重み付けして調整した。
正答率が1~3%くらい上がる感じだが、正しく施行しないと過学習と同じ様になる。
重み付けは1/RMSE^2で実行。1/RMSEでも余り変わらず。
あまりここだけに拘泥するのはよくない。
良い特徴量を作れたほうが強い。
回答提出用加工
TrainとTest+回答提出用(1)を使った学習
分類で良く使われる手法。
精度UPにはつながるが、ええのかこれとは思う。
回答提出
一番いい奴を頼む。
なんでこれ書いたの?
機械学習の一つ一つの手法ばっかりが着目されていて、やることをまとめて書いてある回帰分析の方法がなかったので。
数学や統計の以前に、プロジェクトとしてどうすんのコレ?っていう。
回帰分析の資料がねえ!
分類のタスクがほとんどで、網羅的に書いている文章も少ない。
あとはとっつきやすいように数式はゼロにしてある文章が欲しかったからです。
(たぶん真似して誰かが書いてくれるでしょう)
結果
1問差で2位でした。
コード
まずは基本的な設定と確認。
不要なコードもあるので適宜追加・削除してください。
基本的なモジュール(機能)の読み込み。
# data analysis import pandas as pd import numpy as np from scipy import stats import math, copy # visualization import seaborn as sns # import matplotlib.pyplot as plt from datetime import datetime import statistics %matplotlib inline
最後にmatplotlib(グラフ描写ソフト)の出力をファイル内に行うよう指定。
matplotlibの図に漢字を使うと豆腐になる対策済み。
plt.rcParams['font.family'] = 'IPAexGothic'
顧客から指定のあったカテゴリ変数を設定しておく。他タスクにも応用可能。
master_category = np.array(['管轄区分', '設計区分', '構造1', '構造2', '構造3'])
※一般的なもののみ表示。
エクセルデータだったのでそれで処理。
# read data(学習データ、適用データ)
df_train = pd.read_excel('train.xlsx', encoding='SHIFT-JIS')
df_test = pd.read_excel('test.xlsx', encoding='SHIFT-JIS')
エクセルファイルはSHIFT-JISがほとんどです。忘れると漢字を上手く読み込めないよ。
めんどうなのでtrainとtestをまとめて確認します。
# まとめて確認
df_comb = pd.concat([df_train, df_test])
# trainの先頭から5件(行)表示
df_comb.head(5)
# 基礎情報
print("train shape: %s" % str(df_train.shape))
print("test shape: %s" % str(df_test.shape))
print("comb shape: %s" % str(df_comb.shape))
# 各種統計量の表示
df_comb.describe()
カテゴリ変数設定が合ってるかどうか確認しておく。
for mcl in master_category:
print(mcl)
print(df_comb.iloc[:, df_comb.columns.str.contains(mcl)].columns)
※master_categoryの1要素(文字列)ずつを、df_combの列が含んでいるか確認しています。
欠損値数とその割合を見ておく。
# 欠損値調査
df_nn = df_comb.notnull().sum()
df_nu = df_comb.isnull().sum()
df_all = df_nn + df_nu
df_np = df_nu / df_all * 100
pd.DataFrame({'ALL':df_all, 'Null数':df_nu, 'Null%':df_np}, index=df_comb.columns)
以降加工
決定木用の加工を行う。
加工用にデータフレームをコピーする。
df_ts = df_comb.copy()
コピーしておくと加工に失敗しても手戻りが少ない。
確認時に“1行あたりのNullカラムが多いと価格が下がる”知見を獲得していたので追加。
# Nullカラムが多いと値段が低い傾向にある
if 'Nullカラム数' not in df_ts.columns:
df_ts['Nullカラム数'] = df_ts.isnull().sum(axis=1)
infとかいう困ったちゃんをnanに置き換える
↓
fillnaする(決定木用なのでもともと持っていない値にする。)
# infをNanへ変換 df_ts['合成変数21'] = df_ts['合成変数21'].replace([np.inf, -np.inf], np.nan) df_ts['合成変数21'] = df_ts['合成変数21'].fillna(-1)
なぜか1、0ではなく有、無、Nanの列があったので加工。
無とNanは別モノだよと学習器(木)に教えてあげる。
# 'すごい変数'は「有」「無」Nanで表記されているのでそれぞれ値を振る
df_ts['すごい変数'] = df_ts['すごい変数'].replace({'有': 1, '無': 0, np.nan: -1}).astype('float64')
カテゴリ変数とその他の変数の穴埋めをする。
今回は決定木なので、欠損値を0として設定しておく。
# 残ったカラムの穴埋めを行う
# 決定木の場合外れ値(0等)、線形の場合mean・medianが良いらしい
for i, col in enumerate(df_ts.columns):
# 0の場合スルー
if df_ts[col].isnull().sum() == 0:
continue
# カテゴリ変数の場合
if col in master_category:
num = 0 # 1つの値(欠損値=0)として規定
else: # カテゴリ変数ではない(=連続値)の場合
#num = df_ts[col].dropna().median()
#num = df_ts[col].dropna().mean()
num = 0
print("[%s] fill:%s" % (col, num))
print("→ %.2f~%.2f" % (df_ts[col].dropna().min(), df_ts[col].dropna().max()))
df_ts[col] = df_ts[col].fillna(num)
※計算を早くするためにNull数が0の列はスルーしておく。
※Median・Meanを採用するときは先にdropnaをしてあげるとエラーが出ない。
加工確認
# 値の確認 df_ts.head(5) # 最終確認 df_ts.describe()
ここで列ごとに外れ値を検知して、決定木用に「-1」とする。
ここでは四分位値を指標に外れ値を検出している。
df_dm = df_ts.copy()
for i, col in enumerate(df_dm.columns):
# カテゴリ変数の場合無視
if col in master_category:
continue
# メインカラムの場合除外
if col in ['No', '総合計']:
continue
# 実行
num = df_dm[df_dm[col] != 0][col]
# 四分位値を出力
Q1 = num.quantile(.25)
Q3 = num.quantile(.75)
# IQRでの外れ値検出
IQR = Q3 - Q1
th_ov = Q3 + 1.5 * IQR
th_lw = Q1 - 1.5 * IQR
# 変換
df_target = df_dm[col].values
count = 0
for j in range(df_target.shape[0]):
if df_target[j] > th_ov or df_target[j] < th_lw:
df_target[j] = np.nan
count += 1
df_dm[col] = df_dm[col].replace(np.nan, -1)
# 出力
print("No.%s [%s]" % (i, col))
print("...Target Num is %s" % (num.shape[0]))
print("→ ONLY %.2e~%.2e ... IS NOT %s" % (th_lw, th_ov, count))
その他の方法もあるので一概にこれがいいとは言えない。
※今回の場合これを行うと精度が安定して上がったので採用した。
最後にNull値を持つ列がないか確認する。
# Null値を検出 df_dm[df_dm.isnull().any(axis=1)]
列だと思う。行じゃなかったはず(曖昧)←なんでや
正規化・標準化
今回は正規化を採用(しても決定木では意味はないが)
・・・線形の学習器も並行して使ってみてたから仕方ない!
とりあえず関数化しとこね。
# 正規化を行う
from sklearn.preprocessing import MinMaxScaler, StandardScaler, RobustScaler, Normalizer
scaler = MinMaxScaler()
#scaler = StandardScaler()
#scaler = RobustScaler()
#scaler = Normalizer(copy=True, norm='l2')
def data_normalization_fit(df):
scaler.fit(df.astype('float64'))
def data_normalization_transform(df):
df = pd.DataFrame(data=scaler.transform(df), columns=df.columns, index=df.index)
return df
※ふつーにscaler.fitとscaler.transformでいいと思う。
※ある経緯があってこの形にしているが、現状ではあまり意味はない。
最終確認(shape)
df_dm.shape
学習
combineしていたので分割。
つまり今まででmean埋めをしていると、情報リークになってしまうやり方になっていた。
mean埋めする場合はtrainとtestは分けておくといいと思う。
df_train = df_dm[:df_train.shape[0]] df_test = df_dm[df_train.shape[0]:]
※0埋めと-1埋めしかやってないのでセーフ。
ちゃんと分けられているか確認。
print(df_train.shape, df_test.shape)
相関係数の表示
# 相関係数の表示 fig, ax = plt.subplots(figsize=(20, 20)) sns.heatmap(df_train.corr(), square=True, vmax=1, vmin=-1, center=0)
※実データでは相関が見えない悲しみを背負っていた。
学習前に色々取得。
もちろん要らんやつもある。
# トレーニング用sklearnの読み込み from sklearn.metrics import accuracy_score, roc_curve, auc, confusion_matrix, mean_squared_error from sklearn.model_selection import train_test_split, GridSearchCV, RandomizedSearchCV, cross_val_score, KFold
学習データの作成。
# トレーニングデータ(全体)の作成 y = df_train['総合計'] X = df_train.drop(['総合計', 'No'], axis=1)
ちなみにdf_testの方もデータフレームに入れておく。
変数自動合成・選択の時、手動で入れるのがめっちゃめんどいので。
Z = df_test.drop(['総合計', 'No'], axis=1)
これも上記と理由は同じ。
先に列順をソートしておく。
列の順番変わると学習器がアヘる(というより、列順は変わらないものとして学習している)ので、注意するように。
X = X.astype('float64')
Z = Z.astype('float64')
X = X.sort_index(axis=1, ascending=False)
Z = Z.sort_index(axis=1, ascending=False)
またも確認。
print(X.shape, Z.shape) X.describe()
データ分割。
shuffle入れてもいいけどどっちでもいい。今回は使用せず。
stratifyも今回は層化サンプリング(クラス分類で使用)は必要ないので設定しない。
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0) # , shuffle=True
print('train size: %s, test size: %s' % (X_train.shape,X_test.shape))
正規化(標準化)
# 正規化(情報リーク対策) data_normalization_fit(X_train) X_train = data_normalization_transform(X_train) X_test = data_normalization_transform(X_test)
英語は気にしてはいけない
今回ホールドアウト法とクロスバリデーションを使う。
そのため、クロスバリデーション用のK_Foldを設定しておく。
cv=K_Fold(数字の代わり)のように使う。
K_Fold = KFold(n_splits=3, shuffle=False, random_state=0)
評価関数を作っておく。
上がホールドアウト法用で、下がクロスバリデーション用。
動けば良い。(平均絶対誤差率の10%以内で1point)
# 評価
def accuracy_test(y_pred, y_test):
sum_acc = 0
histgram = []
for i, num in enumerate(y_test):
pred = y_pred[i]
per = (num - pred) / num
histgram.append(per)
if abs(per) <= 0.1:
sum_acc += 1
return [sum_acc, histgram]
# 評価関数を自前で作成する(損失率)
from sklearn.metrics import make_scorer
def func_scoring(y_true, y_pred):
acc = 0
for t, p in zip(y_true, y_pred):
score = (t - p) / t
if abs(score) <= 0.1:
acc += 1
return acc / y_true.shape[0]
色々な書き方を試してみるのも面白い。
学習器を色々インポートして設定しておく。
sklearnのチュートリアルに書いてあるものを一つずつ書いているだけ。
※SGDはデータ量的に全然足りないが試しに使っている。
from sklearn.linear_model import LinearRegression # 重回帰分析
LR = LinearRegression()
from sklearn.linear_model import SGDRegressor # 勾配降下法
SGDR = SGDRegressor(max_iter=1000, tol=1e-3)
from sklearn.linear_model import Lasso # ラッソ(L1)変数の個数を減らすマン
L1R = Lasso()
from sklearn.linear_model import Ridge # リッジ(L2)変数の重みを減らすマン
L2R = Ridge()
from sklearn.linear_model import ElasticNet # L1+L2
L1L2R = ElasticNet()
from sklearn.tree import DecisionTreeRegressor # 決定木
DTR = DecisionTreeRegressor(random_state=0)
from sklearn.ensemble import RandomForestRegressor # ランダムフォレスト回帰
RFR = RandomForestRegressor(n_estimators=100)
from sklearn.svm import SVR # サポートベクター回帰
SVRR = SVR(gamma='auto')
import xgboost as xgb # XGB
XGBR = xgb.XGBRegressor(objective='reg:linear')
# V
XGBR_V = xgb.XGBRegressor(base_score=0.5, booster='gbtree', colsample_bylevel=1, colsample_bytree=1, eval_metric='rmse',
random_state=0, n_estimators=350, max_depth=4, subsample=0.9415106807538888,
learning_rate=0.11288378916846889, gamma=0.0,
reg_lambda=1.0, reg_alpha=0.0,
importance_type='gain', max_delta_step=0, min_child_weight=1,
missing=None, n_jobs=-1, nthread=None, objective='reg:linear', predictor='gpu_predictor',
scale_pos_weight=1, seed=None, silent=True)
from sklearn.ensemble import BaggingRegressor # バギング回帰
BGR_DTR = BaggingRegressor(DTR, n_estimators=100, max_samples=0.3)
チューニング済みのも入れた。
適宜チューニングして最適なものを追加していく。
パイプライン用に読み込んでおく。
クロスバリデーション、グリッドサーチ等時に正規化等を自動的に読み込んでくれるので便利。
# pipe_line from sklearn.pipeline import Pipeline
テストするモデルを設定しておく。
とりあえず適当にするのでなんでも入れてOK。
list_model = {'重回帰':LR, 'SGD':SGDR, 'L1':L1R, 'L2':L2R, 'L1_L2':L1L2R, 'SVR':SVRR
'決定木':DTR, 'ランダムフォレスト回帰':RFR, 'XGB':XGBR, 'XGB_V':XGBR_V, 'バギング(DTR)':BGR_DTR}
ホールドアウト法を実施。
# 各モデルをテスト(ホールドアウト法)
for name, model_test in list_model.items():
# Fit
model_test.fit(X_train, y_train)
# Predict
y_pred_test = model_test.predict(X_test)
# 回答チェック&ヒストグラム化
[sum_acc, histgram] = accuracy_test(y_pred_test, y_test)
# 表示
print("#---------------------------------------------------------#")
print("#", name)
print("#---------------------------------------------------------#")
#plt.hist(histgram, bins=100, range=(-0.6, 0.6))
#plt.show()
print("MAPE Average: %.2f%, Median: %.2f%" % (np.mean(histgram), statistics.median(histgram)))
print("The Accuracy: %.2f%(=%s / %s)" % ((sum_acc / y_test.shape[0]) * 100, sum_acc, y_test.shape[0]))
クロスバリデーションを実施。
# 各モデルをテスト2(CV:K-Fold法)
for name, model_test in list_model.items():
# 表示
print("#---------------------------------------------------------#")
print("#", name)
print("#---------------------------------------------------------#")
pipe_model = Pipeline([("scaler", scaler), ("model", model_test)])
CV = cross_val_score(pipe_model, X, y, cv=3, scoring=make_scorer(func_scoring, greater_is_better=True))
print("Cross-validation scores: %.3f(%s)" % (CV.mean(), CV))
cv=3でなくても別に構わない。
アンサンブル用に適当に選択しておく。
list_model_sel = {'XGB':XGBR, 'XGB_V':XGBR_V}
XGB簡易パラメーターチューニング用に設定。
全て行うと計算回数が20^5*10^2(いくらですかこれ:3億2千万回)を、
10*2+20*5(120回)に削減している。
もちろんn_estimatorsの設定値によって大分変わるが減ったのは間違いない。
cv_list = {
'XGB':
{
'discriminator': xgb.XGBRegressor(objective='reg:linear'),
'random_state': [0],
'booster': ['gbtree', 'gblinear'],
'n_estimators': [100, 150, 200, 250, 300, 350, 400, 450, 500],
'max_depth': [3, 4, 5, 6, 7, 8, 9, 10],
'subsample': 1.1 - 10 ** np.linspace(-1, -0.8, 20), # ~1
'learning_rate': 10 ** np.linspace(-1.2, -0.9, 20),
'gamma': np.linspace(0, 1.0, 20), # 0~
'reg_lambda': 1.1 - 10 ** np.linspace(-1, -0.3, 20), # ~1
'reg_alpha': -0.1 + 10 ** np.linspace(-1, -0.3, 20) # 0~
},
'SVR':
{
'discriminator': SVR(),
'kernel': ['poly', 'rbf', 'sigmoid', 'linear'],
'degree': np.arange(1, 10, 1),
'C': 10 ** np.linspace(-5, 3, 20),
'gamma': np.linspace(0, 1.0, 20),
'epsilon': 10 ** np.linspace(-5, 0, 20)
}
}
ついでにSVR用も設定している。ほんとついでです。(超平面を作り出せるrbfさんがんばれ)
パラメーターチューニングを実行。
記述されている上から順にパラメーターをチューニング→設定、チューニング→設定・・・としている。
for model in cv_list:
# model作成
print("#---------------------------------------------------------#")
print("#", model, "loaded")
print("#---------------------------------------------------------#")
model_test = cv_list[model]['discriminator']
model_name = "model"
pipe_model = Pipeline([("scaler", scaler), (model_name, model_test)])
model_param = cv_list[model].copy()
del model_param['discriminator']
# paramごとにCV
best_param = {}
for param in model_param:
# make
param_one = model_name + "__" + param
param_grid = {}
param_grid[param_one] = model_param[param]
param_grid.update(best_param) # 以前のチューニング結果を反映
print(">> Tuning '%s' is..." % (param))
model_cv = GridSearchCV(pipe_model, param_grid=param_grid, cv=3, scoring=make_scorer(func_scoring, greater_is_better=True),
return_train_score=False, n_jobs=-1, verbose=0)
model_cv.fit(X, y)
# Best
best_param[param_one] = [getattr(model_cv.best_estimator_.steps[1][1], param)]
print('Best Params:', best_param[param_one])
# last
print(">> All Best Params is...")
print(best_param)
終わったらbest_paramを表示してくれる。うれしい。
これで学習は終わり。
変数自動合成(遺伝的アルゴリズム)
遺伝的プログラミングによる特徴量生成でLightGBMの精度向上【kaggle Advent Calendar 11日目】とかいう神が居たので応用した。
※上手く使うととても強い。
※時間はXGBでするととてもかかるので注意。決定木でやるとすごく早い。
※結局神は降臨しなかった。(抜きん出れなかったという意味で)
コピーしてnumpy行列にしておく。
numpy行列なので、列名とかの情報がなくなっているのでsaveしておく。
# numpy配列に変換 X_syn = X.copy().values y_syn = y.copy().values Z_syn = Z.copy().values # 内容保存(加工しなおしに使える) X_save = X.copy() y_save = y.copy() Z_save = Z.copy()
データ分割
XS_train, XS_test, yS_train, yS_test = train_test_split(X_syn, y_syn, test_size=0.2, random_state=0) # , shuffle=True
print('train size: %s, test size: %s' % (XS_train.shape, XS_test.shape))
必要最低限を採用
import random, operator, time from deap import creator, base, gp, tools, algorithms from tqdm import tqdm
※tqdmはfor文の進捗を示すモジュール。要らないと言えば要らない。
seed設定。
random_seed = 0
今回は0にした。(意図はない)
ベースラインスコアを設定しておく。
# ベースラインスコア(train)
clf = XGBR_V
pipe_model = Pipeline([("scaler", scaler), ("model", clf)])
base_train_score = np.mean(cross_val_score(pipe_model, XS_train, yS_train, cv=3,
scoring=make_scorer(func_scoring, greater_is_better=True)))
# test
scaler.fit(XS_train)
clf.fit(scaler.transform(XS_train), yS_train)
[sum_acc, histgram] = accuracy_test(clf.predict(scaler.transform(XS_test)), yS_test)
base_test_score = sum_acc / yS_test.shape[0]
※これ以上のスコアを出す系統を採用するため。
※なかったら変なのでも追加されてしまう。
自作関数も入れておいた。
# 除算関数の定義(左項 / 右項で右項が0の場合1を代入する)
def protectedDiv(left, right):
eps = 1.0e-7
tmp = np.zeros(len(left))
tmp[np.abs(right) >= eps] = left[np.abs(right) >= eps] / right[np.abs(right) >= eps]
tmp[np.abs(right) < eps] = 1.0
return tmp
# log関数の指定
def math_log(a):
eps = 1.0e-7
tmp = np.zeros(len(a))
tmp[a >= eps] = np.log(a[a >= eps])
tmp[a < eps] = 1.0
return tmp
logやexpは特徴量を作り出す時によく使う。
面倒なので(変数組み合わせてもいい変数できないし)、すべて自動でやってもらうおうという怠慢。
詳しくはググってどうぞ。(なお体系的な資料は出てこないもよう)
初期設定。
# 乱数シード設定
random.seed(random_seed)
# 適合度を最大化するような木構造を個体として定義
creator.create("FitnessMax", base.Fitness, weights=(1.0,))
creator.create("Individual", gp.PrimitiveTree, fitness=creator.FitnessMax)
スコア保持用
# scores results = [] # 特徴量数、学習データのscore(K-fold CV)、テストデータのscore exprs = [] # 生成された特徴量の表記
スコア保持用2
# 初期値の生成 n_features = XS_train.shape[1] # 特徴量の数 base_score = base_train_score # ベースラインレートを指定 # メモリ保持 best_expr = 0 best_score = base_score best_train_score = 0 best_test_score = 0
スコア保持用3
nf_plus = 30 # 最大追加特徴量数
合成前最終確認
print("Features: %s" % (n_features))
print("BaseRate: %.2f%" % (base_score * 100))
合成。
変数合成に成功した場合、その変数をXにも追加するがZにも追加しておく。
(手動で入れるととても時間かかって・・・)
for i in tqdm(range(100)): # プログレスバーの表示
# 基礎表示
num_prog = XS_train.shape[1] - X_train.shape[1]
print("# Rank: %s, Last: %s, StartTime: %s" % ((num_prog + 1), (nf_plus - num_prog), datetime.today().strftime("%Y%m%d_%H%M")))
print("Features: %s, Base Score: %.2f%" % (n_features, base_score*100))
# 特徴量が指定数まで増えたら終了
if n_features >= XS_train.shape[1] + nf_plus:
print("Features are Over.")
break
# 構文木として利用可能な演算の定義
pset = gp.PrimitiveSet("MAIN", n_features)
pset.addPrimitive(operator.add, 2) # A+B
pset.addPrimitive(operator.sub, 2) # A-B
pset.addPrimitive(operator.mul, 2) # A*B
pset.addPrimitive(protectedDiv, 2) # A/B
pset.addPrimitive(operator.neg, 1) # -A
pset.addPrimitive(np.cos, 1) # cosA
pset.addPrimitive(np.sin, 1) # sinA
pset.addPrimitive(np.tan, 1) # tanA
pset.addPrimitive(math_log, 1) # log1pA
# 関数のデフォルト値の設定
toolbox = base.Toolbox()
toolbox.register("expr", gp.genHalfAndHalf, pset=pset, min_=1, max_=3)
toolbox.register("individual", tools.initIterate, creator.Individual, toolbox.expr)
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
toolbox.register("compile", gp.compile, pset=pset)
# 評価関数の設定
# 新しく生成した変数を元の変数に加えてK-fold CVを求める
def eval_genfeat(individual):
func = toolbox.compile(expr=individual)
features_train = [XS_train[:,i] for i in range(n_features)]
new_feat_train = func(*features_train)
XS_train_tmp = np.c_[XS_train, new_feat_train]
return np.mean(cross_val_score(pipe_model, XS_train_tmp, y_train, cv=3, n_jobs=-1,
scoring=make_scorer(func_scoring, greater_is_better=True))), # このタプル化コンマは消さない
# 評価、選択、交叉、突然変異の設定
# 選択はサイズ10のトーナメント方式、交叉は1点交叉、突然変異は深さ2のランダム構文木生成と定義
toolbox.register("evaluate", eval_genfeat) # 評価関数
toolbox.register("select", tools.selTournament, tournsize=10) # 選択方法
toolbox.register("mate", gp.cxOnePoint) # 交叉
toolbox.register("expr_mut", gp.genFull, min_=0, max_=2) # 突然変異
toolbox.register("mutate", gp.mutUniform, expr=toolbox.expr_mut, pset=pset) # ?
# 構文木の制約の設定
# 交叉や突然変異で深さ5以上の木ができないようにする
toolbox.decorate("mate", gp.staticLimit(key=operator.attrgetter("height"), max_value=5)) # 交叉
toolbox.decorate("mutate", gp.staticLimit(key=operator.attrgetter("height"), max_value=5)) # 突然変異
# 世代ごとの個体とベスト解を保持するクラスの生成
pop = toolbox.population(n=300) # 個体...300
hof = tools.HallOfFame(1) # ベスト解
# 統計量の表示設定
stats_fit = tools.Statistics(lambda ind: ind.fitness.values)
stats_size = tools.Statistics(len)
mstats = tools.MultiStatistics(fitness=stats_fit, size=stats_size) # mstats基礎設定
mstats.register("avg", np.mean)
mstats.register("std", np.std)
mstats.register("min", np.min)
mstats.register("max", np.max)
# 進化の実行
# 交叉確率50%、突然変異確率10%、10世代まで進化
start_time = time.time()
pop, log = algorithms.eaSimple(pop, toolbox, 0.5, 0.1, 10, stats=mstats, halloffame=hof, verbose=True)
end_time = time.time()
# ベスト解の保持
best_expr = hof[0]
best_score = mstats.compile(pop)["fitness"]["max"]
# K-fold CVのscoreが前ステップのscoreを超えていた場合
# 生成変数を学習、テストデータに追加し、base_scoreを更新する
if best_score > base_score:
# 生成変数の追加
func = toolbox.compile(expr=best_expr)
features_train = [XS_train[:,i] for i in range(n_features)]
features_test = [XS_test[:,i] for i in range(n_features)]
features_Z = [Z_syn[:,i] for i in range(n_features)]
new_feat_train = func(*features_train)
new_feat_test = func(*features_test)
new_feat_Z = func(*features_Z)
XS_train = np.c_[XS_train, new_feat_train]
XS_test = np.c_[XS_test, new_feat_test]
Z_syn = np.c_[Z_syn, new_feat_Z]
# テストscoreの計算(プロット用)
# train
best_train_score = np.mean(cross_val_score(pipe_model, XS_train, yS_train, cv=3, scoring=make_scorer(func_scoring, greater_is_better=True)))
# test
scaler.fit(XS_train)
clf.fit(scaler.transform(XS_train), yS_train)
[sum_acc, histgram] = accuracy_test(clf.predict(scaler.transform(XS_test)), yS_test)
best_test_score = sum_acc / yS_test.shape[0]
# base_scoreの更新と特徴量数の再計算
base_score = best_score
n_features = XS_train.shape[1]
# 表示と出力用データの保持
print("Go to Next... 計算所要時間 %.1f分" % ((end_time - start_time) / 60))
print("Features: %s, Best Score: %.2f%" % (n_features, best_score*100))
print("Train: %.2f%, Test: %.2f%" % (best_train_score*100, best_test_score*100))
results.append([n_features, best_score, best_train_score, best_test_score])
exprs.append(best_expr)
XGBの場合2000行のデータを1周り計算するのに、8コア使用PCで1時間くらいかかる。
計算コストがバカにならないのでチューニング済決定木の方がいい気がする。
# 結果の出力
print("# Results")
print("Baseline train: %.2f%" % (base_train_score*100))
print("Baseline test: %.2f%" % (base_test_score*100))
print("Best train: %.2f%" % (results[-1][1]*100))
print("Best test: %.2f%" % (results[-1][3]*100))
# 結果のプロット
res = np.array(results)
plt.plot(res[:,0], res[:,1], "o-", color="b", label="train(3-fold CV)")
plt.plot(res[:,0], res[:,3], "o-", color="r", label="test")
plt.plot(X_train.shape[1], base_train_score, "d", color="b", label = "train baseline(3-fold CV)")
plt.plot(X_train.shape[1], base_test_score, "d", color="r", label = "test baseline")
plt.xlim(X_train.shape[1]-1, XS_train.shape[1]+1)
plt.grid(which="both")
plt.xlabel('n_features')
plt.ylabel('score')
plt.legend(loc="lower right")
#plt.savefig("gp_featgen.png")
とても大事。
再現性を取るためにこれを出力しておかないと死ぬ。
# 生成した構文木の出力
gp_col = []
print("# Generated feature expression")
for i in range(XS_train.shape[1] - X_train.shape[1]):
#for i in range(XS_train.shape[1] - 146):
col_name = "GP_COL" + str(i)
gp_col.append(col_name)
print("+%s = %s" % (col_name, exprs[i]))
下記でもよい。
# 過去保存用
for i in range(len(exprs)):
print(i, exprs[i])
X、y、Zを戻す。
# 元に戻す X = pd.DataFrame(np.concatenate([XS_train, XS_test], 0), index=X_save.index, columns=np.concatenate([X_save.columns, gp_col])) y = pd.Series(np.concatenate([yS_train, yS_test], 0), index=y_save.index) Z = pd.DataFrame(Z_syn, index=Z_save.index, columns=np.concatenate([Z_save.columns, gp_col])) print(X.shape, y.shape, Z.shape)
変数選択(簡易)
後退的選択法の簡易版を実装している。
XGBで重要度の低い変数から落として、精度が上がれば正式採用。
X_auto = X.copy() y_auto = y.copy() Z_auto = Z.copy()
XGBを学習させ、重要度を測定。
# モデル選択(チューニング済み)
auto_model = XGBR_V
pipe_model = Pipeline([("scaler", scaler), ("model", auto_model)])
auto_CV = cross_val_score(pipe_model, X_auto, y_auto, cv=K_Fold, scoring=make_scorer(func_scoring, greater_is_better=True),
n_jobs=-1, verbose=2)
# ベースレートの指定
auto_base_rate = auto_CV.mean()
print("base_rate:", auto_base_rate)
# 特徴量の重要度を測定 features_imp = pd.Series(dict(zip(X_auto.columns, auto_model.feature_importances_))) features_imp.sort_values(ascending=True, inplace=True)
# 表示 plt.figure(figsize=(10, 30)) plt.barh(features_imp.index, features_imp)
初期設定
# 自動用Series(途中保存可能) auto_rank = pd.Series() auto_var = pd.Series(X_auto.columns) # 保存用list auto_graph = [] auto_columns = [] auto_data = []
滅茶苦茶単純なのでスルー
# AUTO_VAR
for i, col_var in enumerate(features_imp.index):
auto_ranks = {}
print('# Rank', i, 'Start.', 'Len:', str(auto_var.shape[0] - auto_rank.shape[0]),'Time:',datetime.today().strftime("%Y%m%d_%H%M"))
# 変数を1残す
if auto_var.shape[0] <= 1:
break
# 特徴選択(Backward Selection)
col_drop = pd.concat([auto_rank, pd.Series([col_var])])
# X選択
X_sel = X_auto.drop(col_drop.values, axis=1)
# Fit
auto_CV = cross_val_score(pipe_model, X_sel, y_auto, cv=3, scoring=make_scorer(func_scoring, greater_is_better=True),
n_jobs=-1, verbose=2)
auto_acc = auto_CV.mean()
# 解答&削除判定
print("→ Col:%s, Point:%.4f(%.4f)" % (col_var, auto_acc, (auto_acc - auto_base_rate)))
if auto_acc > auto_base_rate:
auto_rank = pd.concat([auto_rank, pd.Series(col_var)])
auto_var = auto_var[auto_var != col_var]
print("→→ Dropped!")
auto_base_rate = auto_acc
# グラフに追加
auto_columns.append(col_var)
auto_graph.append(auto_acc)
auto_data.append(X_sel.columns)
列drop → クロスバリデーションして精度検証 → それより上なら正式採用
# プロット
plt.plot(range(1, len(auto_graph) + 1), auto_graph, label="Correct Num")
plt.xlabel('Epochs')
plt.ylabel('Correct Num')
plt.legend()
plt.show()
いろいろ保存
arg_max = int(np.argmax(auto_graph))
print('No.', arg_max, 'Correct:', auto_graph[arg_max])
print('Columns:', auto_data[arg_max])
# save_cols
save_cols = auto_data[arg_max]
再現性を取るために残っている変数と落とした変数を表示する。
print("Save:", save_cols.values)
print("Drop:", auto_rank)
元に戻す。
# 再変換 y = y_auto.copy() X = X_auto[save_cols] Z = Z_auto[save_cols]
アンサンブル(適当)
実際これでいいのかとは思っている。精度UPの実績はあるが。
# 線形回帰の実装
LR_model = LinearRegression()
# 辞書の実装
EMB_DICT = {}
学習の最後で選んだ適当な学習器を使ってアンサンブルする。
# 辞書の追加 EMB_DICT.update(list_model_sel)
とりあえずまずはどれくらい当たっているかグラフで確認する。
data_emb = []
rmse_emb = []
for name, model in EMB_DICT.items():
print("#", name)
model.fit(X_train, y_train)
data_x = model.predict(X_test).reshape(-1, 1)
data_y = y_test.values.reshape(-1, 1)
LR_model.fit(data_x, data_y)
[sum_acc, histgram] = accuracy_test(data_x, data_y)
print("回帰係数:%.2f, 切片:%.2f" % (LR_model.coef_, LR_model.intercept_))
print("R^2:%.2f, SumAcc:%.2f" % (LR_model.score(data_x, data_y), sum_acc / data_y.shape[0] * 100))
plt.scatter(data_x, data_y, s=100, c="yellow", alpha=0.5, linewidths="2", edgecolors="orange")
plt.plot(data_x, LR_model.predict(data_x))
plt.show()
data_emb.append(data_x)
rmse_emb.append(np.sqrt(mean_squared_error(data_y, data_x)))
ついでにアンサンブルデータも保存しておく。
今回は平均アンサンブルと重み付け(1/RMSE^2)アンサンブルを実装している。
平均アンサンブルは精度上昇に貢献しなかった。
model_emb = np.average(data_emb, axis=0)
print("# emb")
data_x = model_emb
data_y = y_test.values.reshape(-1, 1)
LR_model.fit(data_x, data_y)
[sum_acc, histgram] = accuracy_test(data_x, data_y)
print("回帰係数:%.2f, 切片:%.2f" % (LR_model.coef_, LR_model.intercept_))
print("R^2:%.2f, SumAcc:%.2f" % (LR_model.score(data_x, data_y), sum_acc / data_y.shape[0] * 100))
plt.scatter(data_x, data_y, s=100, c="yellow", alpha=0.5, linewidths="2", edgecolors="orange")
plt.plot(data_x, LR_model.predict(data_x))
plt.show()
重み付けアンサンブル
emb_weights = []
for i, val in enumerate(rmse_emb):
print("%s: %s" % (i+1, val))
emb_weights.append(1/pow(val, 2))
model_emb_weights = np.average(data_emb, axis=0, weights=emb_weights)
print("# emb weights")
data_x = model_emb_weights
data_y = y_test.values.reshape(-1, 1)
LR_model.fit(data_x, data_y)
[sum_acc, histgram] = accuracy_test(data_x, data_y)
print("回帰係数:%.2f, 切片:%.2f" % (LR_model.coef_, LR_model.intercept_))
print("R^2:%.2f, SumAcc:%.2f" % (LR_model.score(data_x, data_y), sum_acc / data_y.shape[0] * 100))
plt.scatter(data_x, data_y, s=100, c="yellow", alpha=0.5, linewidths="2", edgecolors="orange")
plt.plot(data_x, LR_model.predict(data_x))
plt.show()
とはいえコード自体は簡単なものである。
加工と実装。
AP_X = data_normalization_transform(X)
AP_Z = data_normalization_transform(Z)
data_emb_apply = []
for name, model in EMB_DICT.items():
print("#", name, "Apply")
model.fit(AP_X, y)
data_x = model.predict(AP_Z).reshape(-1, 1)
data_emb_apply.append(data_x)
model_emb_apply = np.average(data_emb_apply, axis=0, weights=emb_weights) answer = model_emb_apply.flatten()
提出前加工
ふつう。工夫はない。
df_answer = pd.DataFrame({'No' : df_test['No'].values,
'総合計' : answer })
# 提出用データ作成
df_answer.to_csv('Sub_'+datetime.today().strftime("%Y%m%d_%H%M")+'.csv', index=False, encoding="SHIFT_JIS")
終わりません。
答えの合成
黒魔術的なモノですが、効果はあります。
予測した値を使ってさらに予想する方法です。
NZc = pd.concat([df_answer, Z], axis=1).drop('No', axis=1)
NXc = X.copy()
Nyc = pd.DataFrame(y.copy(), columns=['総合計'], index=NXc.index)
NData =pd.concat([pd.concat([Nyc, NXc], axis=1), NZc], axis=0)
print(NData.shape) NData.head()
# トレーニングデータ(全体)の作成 Ny = NData['総合計'] NX = NData.drop(['総合計'], axis=1)
data_emb = []
rmse_emb = []
for name, model in EMB_DICT.items():
print("#", name)
model.fit(NX_train, Ny_train)
data_x = model.predict(NX_test).reshape(-1, 1)
data_y = Ny_test.values.reshape(-1, 1)
LR_model.fit(data_x, data_y)
[sum_acc, histgram] = accuracy_test(data_x, data_y)
print("回帰係数:%.2f, 切片:%.2f" % (LR_model.coef_, LR_model.intercept_))
print("R^2:%.2f, SumAcc:%.2f" % (LR_model.score(data_x, data_y), sum_acc / data_y.shape[0] * 100))
plt.scatter(data_x, data_y, s=100, c="yellow", alpha=0.5, linewidths="2", edgecolors="orange")
plt.plot(data_x, LR_model.predict(data_x))
plt.show()
data_emb.append(data_x)
rmse_emb.append(np.sqrt(mean_squared_error(data_y, data_x)))
emb_weights = []
for i, val in enumerate(rmse_emb):
print("%s: %s" % (i+1, val))
emb_weights.append(1/pow(val, 2))
手順をやり直しているだけなのでコメントのしようがない。
model_emb_weights = np.average(data_emb, axis=0, weights=emb_weights)
print("# emb weights")
data_x = model_emb_weights
data_y = Ny_test.values.reshape(-1, 1)
LR_model.fit(data_x, data_y)
[sum_acc, histgram] = accuracy_test(data_x, data_y)
print("回帰係数:%.2f, 切片:%.2f" % (LR_model.coef_, LR_model.intercept_))
print("R^2:%.2f, SumAcc:%.2f" % (LR_model.score(data_x, data_y), sum_acc / data_y.shape[0] * 100))
plt.scatter(data_x, data_y, s=100, c="yellow", alpha=0.5, linewidths="2", edgecolors="orange")
plt.plot(data_x, LR_model.predict(data_x))
plt.show()
AP_NX = data_normalization_transform(NX) AP_Z = data_normalization_transform(Z)
data_emb_apply = []
for name, model in EMB_DICT.items():
print("#", name, "Apply")
model.fit(AP_NX, Ny)
data_x = model.predict(AP_Z).reshape(-1, 1)
data_emb_apply.append(data_x)
model_emb_apply = np.average(data_emb_apply, axis=0, weights=emb_weights)
answer = model_emb_apply.flatten()
df_answer = pd.DataFrame({'No' : df_test['No'].values,
'総合計' : answer })
# 提出用データ作成
df_answer.to_csv('Sub_'+datetime.today().strftime("%Y%m%d_%H%M")+'_2.csv', index=False, encoding="SHIFT_JIS")
おわり
最後に
意外と超大作になってしまった。(文字数3万文字越えって・・・)
jupyterコードについては、めちゃめちゃデータ(守秘義務)が表示されているので社内のみで共有します。申し訳ございません。
最後まで見ていただき、ありがとうございました。